Центром описанной окружности треугольника является точка пересечения срединных перпендикуляров.
Для остроугольного треугольника этот центр будет в треугольнике.
Построение.
Построить нужный треугольник не составляет труда.
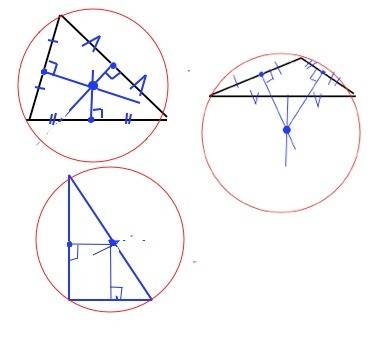
1) Для остроугольного треугольника центр описанной окружности будет внутри треугольника. .
Измерьте линейкой каждую сторону треугольника и найдите ее середину. С угольника ( у него есть прямой угол) проведите из середины каждой стороны прямые. Точка их пересечения - искомый центр описанной окружности.
Расстояние от него до вершин треугольника равны радиусу описанной окружности.
2) Для тупоугольного треугольника построение будет таким же, но срединные перпендикуляры пересекутся ВНЕ треугольника.
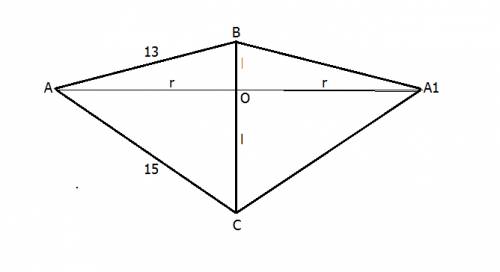
3) Для прямоугольного треугольника достаточно найти середину гипотенузы, т.к. срединные перпендикуляры пересекаются именно в этой точке. Полезно запомнить, что центром описанной вокруг прямоугольного треугольника окружности является середина его гипотенузы, т.к. расстояния от нее до вершин треугольника равны.
Как это выглядит, дано в приложении.
1. Объясните, какую фигуру называют многоугольником.
Любой многоугольник — это плоская замкнутая ломаная.
2. Что называют периметром многоугольника?
Периметр — это сумма всех сторон многоугольника.
3. Что называют диагональю многоугольника?
Диагональю многоугольника называют любой отрезок — соединяющий вершины не прилежащих к одной стороне двух углов.
4. Какой многоугольник называют выпуклым?
Многоугольник, чъи все точки лежат по одну сторону от любой прямой, проходящей через 2 его соседние вершины — называется выпуклым.
5. Как расположен выпуклый многоугольник относительно любой прямой, содержащую его сторону?
Расположен он в одной полуплоскости.
6. Чему равна сумма углов выпуклого n-угольника?
Формула вычисления суммы углов n-угольника: s = 180(n-2).
n — число углов/сторон.
s — сумма углов.
7. Какой круг называют описанным вокруг многоугольника?
Круг называют описанным вокруг многоугольника в том случае, если вершины многоугольника лежат на окружности.
8. Какая точка является центром окружности, описанной около многоугольника?
Точка пересечения серединных перпендикуляров к сторонам — называется центром описанной окружности около мноугольника.
9. Какой круг называют вписанным в многоугольник?
Круг называют вписанным в мноугольник, если все стороны мноугольника касаются окружности.
10. Какая точка является центром окружности, вписанной в многоугольник?
Точка пересечения всех биссектрис многоугольника — называется центром вписанной окружности.