Из этого невнятного условия можно (с трудом) догадатся, что все боковые ребра пирамиды наклонены к основанию под 60 градусов (если это не так - поправьте :)).
В основании равнобедренный прямоугольный треугольник с гипотенузой 4, радиус описанной окружности равен 4/2 = 2. Площадь основания равна 2*4/2 = 4.
Высота пирамиды, радиус описанной окружности и боковое ребро образуют прямоугольный треугольник с углом 60 градусов (противолежащим высоте пирамиды).
Это следует из того, что все ребра равнонаклонены. Пусть М - проекция S на АВС. Тогда все прямоугольные треугольники SMA, SMB, SMC равны (по катету и противолежащему острому углу) => S равноудаленa от вершин => проекция вершины S на АВС равноудалена от вершин А, В, С, то есть АМ = ВМ = СМ - радиус окружности, описанной вокруг АВС.
Таким образом высота пирамиды Н = 2*tg(60) = 2*корень(3).
Объем пирамиды (1/3)*4*2*корень(3) = 8*корень(3)/3
Следует понимать :)) что в этой задаче вершина S проектируется на основание АВС точно в середину М гипотенузы ВС, то есть боковая грань SBC перпендикулярна основанию АВС, и высота пирамиды SM лежит в этой боковой грани :))
Боковое ребро L = 12см,
Высота пирамиды: Н = L·sin60° = 12·0.5√3 = 6√3(cм)
Радиус описанной окружности треугольного основания: R = L·cos60° = 12·0.5 = 6(см)
Сторона а правильного треугольника, лежащего в основании: а = R·√3 = 6√3(см)
высота треугольного основания: h = a·sin 60° = 6√3·0.5√3 = 9(cм)
Площадь основания Sосн = 0.5a·h = 0.5· 6√3 · 9 = 27√3(cм²)
Апофема (высота боковой грани) А² = L² - (0.5a)² = 144 - 27 = 117
A = 3√13(cм)
Площадь боковой грани: Sгр = 0,5а·А = 0,5·6√3·3√13 = 9√39(см²)
Площадь боковой поверхности
Sбок = 3·Sгр = 3·9√39 = 27√39(см²)
Площадь поверхности пирамиды S = Sосн + Sбок = 27√3 + 27√39 =
= 27√3(1 + √13) (см²)
Объём пирамиды: V = 1/3 Sосн ·Н = 1/3 · 27√3 · 6√3 = 162(см³)
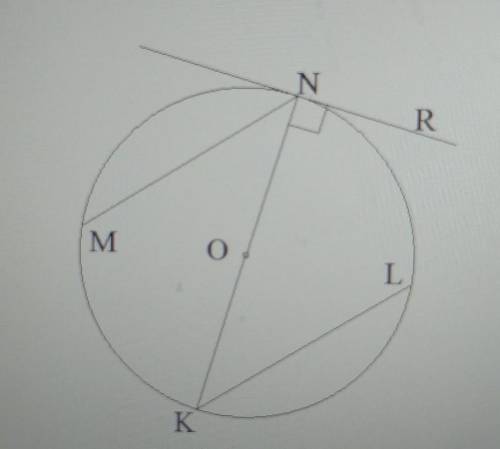
NK
Объяснение:
10000000000000000000%