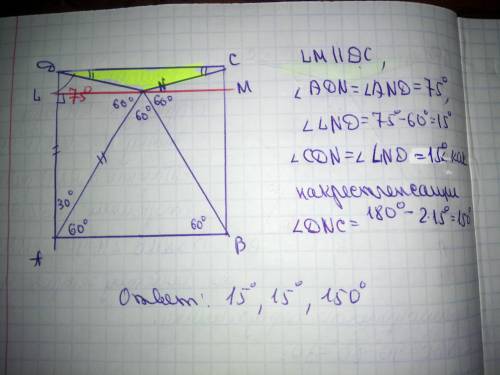
15°, 150° и 15°
Объяснение:
Треугольник ABN - равносторонний, т.е. AB=AN=BN
Но ABCD - квадрат => AB=AN=BN=BC=CD=AD
Рассмотрим треугольник ADN:
<A=90°-<BAN = 90°-60° =30°
AD=AN => треугольник ADN - равносторонний
Значит, <ADN=<AND=(180°-30°)/2 = 75°
Рассмотрим треугольник BCN:
<B=90°-<ABN = 90°-60° =30°
BC=BN => треугольник BCN - равносторонний
Значит, <BNC=<BCN=(180°-30°)/2 = 75°
Рассмотрим треугольник DNC:
<CDN = 90°-<ADN = 90°-75° = 15°
<DCN = 90°-<BCN = 90°-75° = 15°
<DNC = 360° -<AND-<ANB-<BNC = 360°-75°-60°-75° = 150°


Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º, значит ВСД+СДА=180, СДА=180-30=150. Теперь находим угол ВДА=150-75(угол ВДС=75, из дано), значит угол ВДА=75
И угол АВД тоже равен 75, так как 180-30-75=75. Значит треугольник АВД и треугольник ВСД равнобедренный с боковыми сторонами АВ и АД, ВСи СД. Сумма длин сторон АВ и АД равна половине периметра, а он равен 40 см., также мы уже знаем, что эти стороны равны, значит АВ=АД=40/2/2=10 см
ответ: все стороны параллелограмма по 10 см, а углы 30,150,30,150