площадь трапеции равна 63cos31° + 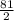 sin62° , что приблизительно равно 89.76
sin62° , что приблизительно равно 89.76
Объяснение:
Достроим рисунок высотами BE и CF.
Отметим, что площадь трапеции ABCD будет совпадать с площадью прямоугольника AFCG = AF*CF = (AE+EF)*BE = (7+AE)*BE
∠ABC=∠CBD=121° , ∠EBC=90° значит ∠ABE=31°
В прямоугольном треугольнике ABE
sin∠ABE=AE/AB ⇒ sin31°=AE/9 ⇒ AE=9*sin31°
cos∠ABE=BE/AB ⇒ cos31°=BE/9 ⇒ BE=9*cos31°
Значит искомая площадь = (7+AE)*BE = (7+9*sin31°)*9*cos31° =
= 63cos31° + 81sin31°cos31° = 63cos31° + 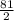 sin62° ≈ 89.76
sin62° ≈ 89.76

Если в задании нужно найти все таки диагональ прямоугольника, тогда:
обозначим как х одну сторону прямоугольник, как у вторую сторону.
Периметр это сумма длин все сторон, т.е
2х+2у=14
Площадь это произведение длин сторон, т.е:
ху=12
Получили систему
Упростим ее разделив 1 уравнение на 2, получим
из 1го уравнение выразим х получим что х=7-у, подставим во второе, получим
(7-у)у=12
Раскрываем скобки, переносим все в левую часть, домножаем на -1 (чтобы было удобнее считать), получам:
Решаем квадратное уравнение.
получаем слудующие корни:
Теперь находим х, из уравнения х=7-у, получаем:
Так как у нас прямоугольник, то его диагональ будет являться гипотенузой прямоугольного треугольника с катетами х и у.
Гипотенуза находится по теореме Пифагора:
Отрицательное значение нам не подходит, значит d=5 (это получается если мы возьмем любую пару решений, как (х1,у1) так и (х2,у2))
ответ: d=5