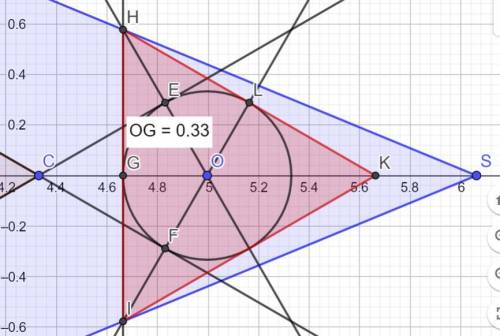
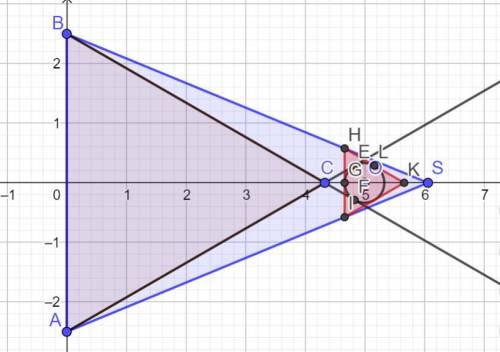
После внимательного прочтения задания стало ясно, что цилиндр, основание которого находится за пределами основания пирамиды, прорезает боковое ребро CS и 2 боковые грани АCS и ВCS.
Верхнее основание цилиндра касается всех боковых граней в точках F, G, L.
Так как в основании правильный треугольник, то и в сечении пирамиды на уровне верхнего основания цилиндра, тоже правильный треугольник. Окружность верхнего основания цилиндра вписана в этот треугольник.
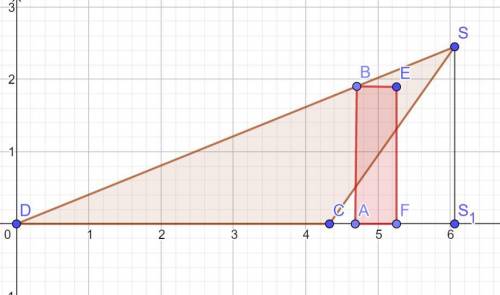
Проведём осевое сечение пирамиды и цилиндра перпендикулярно АВ. Получим треугольник CSD, где D - середина АВ.
SD = √(7² - (5/2)²) = √(49 - (25/4) = √171/2.
CD = 5√3/2 как высота правильного треугольника.
Угол SDС - это угол наклона боковой грани АВS к основанию.
Основа решения задачи – в равенстве высот точек касания верхней основы цилиндра граней ABS и CBS (из за симметрии граней CBS и CАS рассматриваем одну).
Н– высота цилиндра, R – радиус основания.
cos SDС = (( 5√3/2)² + (√171/2)²) - 32/(2* (5√3/2)* (√171/2)) = 210/(30√(3*171)) = 7√57/57.
sin SDС = √(1 – (7√57/57)2) = 2√(2*57)/57.
tg SDС = 2√(2*57)*57/(57*7*√57) = 2√2/7.
Точка с высотой, равной Н на грани BCS, отстоит в плане от линии пересечения с плоскостью основания на величину 2R. Найдём тангенс угла наклона грани BCS.
Найдём проекцию высоты этой грани из точки S на основание.
Сначала находим высоту SS1 точки S:
SS1 = SD*sin SDС = (√171/2) * (2√(2*57)/57) = √(3*57)/2) * (2√(2*57)/57) = √6.
Проекция CS на основание равна: CS1 = √(32 – (√6)2) = √(9 – 6) = √3.
Тогда проекция высоты грани BCS на основание равна половине CS1 или (√3/2) (катет против угла в 30 градусов равен половине гипотенузы).
Тангенс угла наклона грани BCS равен: tg α = √6/(√3/2) = 2√2.
Записываем равенство высот на гранях: (CD + R)* tg SDС = 2R* tg α.
Подставим данные.
(5√3/2 + R)*( 2√2/7) = 2R*2√2. Приведём к общему знаменателю 7.
5√6 + 2R√2 = 28R√2,
26R√2 = 5√6,
R = 5√6/(26√2) = 5√3/26 ≈ 0,333087.
Прилагаемые рисунки даны:
- один в виде осевого сечения,
- второй в виде общего плана (это вид сверху),
- третий это деталь плана с цилиндром.
После внимательного прочтения задания стало ясно, что цилиндр, основание которого находится за пределами основания пирамиды, прорезает боковое ребро CS и 2 боковые грани АCS и ВCS.
Верхнее основание цилиндра касается всех боковых граней в точках F, G, L.
Так как в основании правильный треугольник, то и в сечении пирамиды на уровне верхнего основания цилиндра, тоже правильный треугольник. Окружность верхнего основания цилиндра вписана в этот треугольник.
Проведём осевое сечение пирамиды и цилиндра перпендикулярно АВ. Получим треугольник CSD, где D - середина АВ.
SD = √(7² - (5/2)²) = √(49 - (25/4) = √171/2.
CD = 5√3/2 как высота правильного треугольника.
Угол SDС - это угол наклона боковой грани АВS к основанию.
Основа решения задачи – в равенстве высот точек касания верхней основы цилиндра граней ABS и CBS (из за симметрии граней CBS и CАS рассматриваем одну).
Н– высота цилиндра, R – радиус основания.
cos SDС = (( 5√3/2)² + (√171/2)²) - 32/(2* (5√3/2)* (√171/2)) = 210/(30√(3*171)) = 7√57/57.
sin SDС = √(1 – (7√57/57)2) = 2√(2*57)/57.
tg SDС = 2√(2*57)*57/(57*7*√57) = 2√2/7.
Точка с высотой, равной Н на грани BCS, отстоит в плане от линии пересечения с плоскостью основания на величину 2R. Найдём тангенс угла наклона грани BCS.
Найдём проекцию высоты этой грани из точки S на основание.
Сначала находим высоту SS1 точки S:
SS1 = SD*sin SDС = (√171/2) * (2√(2*57)/57) = √(3*57)/2) * (2√(2*57)/57) = √6.
Проекция CS на основание равна: CS1 = √(32 – (√6)2) = √(9 – 6) = √3.
Тогда проекция высоты грани BCS на основание равна половине CS1 или (√3/2) (катет против угла в 30 градусов равен половине гипотенузы).
Тангенс угла наклона грани BCS равен: tg α = √6/(√3/2) = 2√2.
Записываем равенство высот на гранях: (CD + R)* tg SDС = 2R* tg α.
Подставим данные.
(5√3/2 + R)*( 2√2/7) = 2R*2√2. Приведём к общему знаменателю 7.
5√6 + 2R√2 = 28R√2,
26R√2 = 5√6,
R = 5√6/(26√2) = 5√3/26 ≈ 0,333087.
Прилагаемые рисунки даны:
- один в виде осевого сечения,
- второй в виде общего плана (это вид сверху),
- третий это деталь плана с цилиндром.



У каждого из 8 шаров (сколько вершин у куба, столько шаров) внутри куба лежит 1/8 часть объема, остальное - снаружи. Поэтому сумма объемов частей шаров внутри куба равна объему одного шара, то есть
Объем части куба вне шаров 1/2, значит и объем внутри шаров 1/2.
Часть ребра вне шара равна
(R приблизительно равен 0,492372510921348, а искомая часть ребра приблизительно равна 0,0152549781573035;
R меньше 1/2, то есть шары не пересекаются, что оправдывает предыдущий расчет - если бы шары пересекались, при сложении объемов общие части учитывались бы дважды. То есть если бы получилось R > 1/2, то решение было неверное).