а) х² +5х - 6
Решим уравнение
х² +5х - 6=0
D=25+24=49
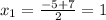
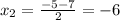
х² +5х - 6=(x-1)(X+6)
б) 3х² + 5х - 8
Решим уравнение
3х² + 5х - 8=0
D=25+96=121
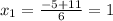
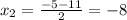
3х² + 5х - 8=3(x-1)(x+8)
Упростим выражение 1 - sin (2 * a) - cos (2 * a).
Для того, чтобы упростить выражение, используем следующие формулы тригонометрии:
sin^2 x + cos^2 x = 1;
cos (2 * x) = cos^2 x - sin^2 x;
sin (2 * x) = 2 * sin x * cos x.
Тогда получаем:
1 - sin (2 * a) - cos (2 * a) = sin^2 a + cos^2 a - (2 * sin a * cos a) - (cos^2 a - sin^2 a) = sin^2 a + cos^2 a - 2 * sin a * cos a - cos^2 a + sin^2 a;
Сгруппируем подобные значения.
(sin^2 a + sin^2 a) + (cos^2 a + cos^2 a) - 2 * sin a * cos a = 2 * sin^2 a - 2 * sin a * cos a = 2 * sin a * (sin a - cos a).
Объяснение:
Представим 4=4*1=4(sin²x+cos²x)=4sin²x+4cos²x
cos2x=cos²x-sin²x
5 22cos²x sin²x-5 22 cos²x sin²x - 5 (sin²x+cos²x)²
22cos²x - = =
sin²x sin²x sin²x
22sin²x cos²x-5sin⁴x-10sin²x cos²x-5cos⁴x 12sin²x cos²x-5sin⁴x-5cos⁴x
= =
sin²x sin²x
Уравнение будет иметь вид:
(4sin²x+4cos²x)sin²x+(9cos²x-9sin²x) sin²x=12sin²x cos²x-5sin⁴x-5cos⁴x
ОДЗ: sin²x≠0, x≠πn, n∈Z
4sin⁴x+4sin²x cos²x+9sin²x cos²x-9sin⁴x-12sin²x cos²x+5sin⁴x+5cos⁴x=0
19sin²x cos²x+5cos⁴x=0
cos²x(19sin²x+5cos²x)=0
1)cosx=0, x=π/2+πk, k∈Z
2)19sin²x+5cos²x=0, Делим на cos²x≠0
19tg²x+5=0, tg²x=-5/19<0 ⇒ нет решений (квадрат числа не может быть отрицательным)
ответ: x=π/2+πk, k∈Z
а) D = 25 + 4* 6 = 25 + 24 = 49
- 5 + 7 2
х 1 = = = 1(доказано)
2 2
х 2 =- 5 - 7
= - 6
2