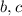Геометрия: 2. Напиши имя учёного древнего мира (до нашей эры):

2. Напиши имя учёного древнего мира (до нашей эры):

👇

Увидеть ответ

Ответ:

BratiSHkaXD

28.05.2022

На фото изображен Евклид

4,5(3 оценок)

Открыть все ответы

Ответ:

cat2522

28.05.2022

Для начало выведем некие следствия, пусть наши основания большее и меньшее соответственно равны b,c

. Пусть высота

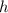тогда по условию
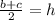$\frac{b+c}{2}=h\\
$ . Заметим что из условия следует что трапеция РАВНОБЕДРЕННАЯ , так как только около нее можно описать окружность . Следовательно обозначим боковые стороны как

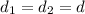, диагонали у трапеции равны $d_{1}=d_{2}=d$ . Как известно у равнобедренной трапеций если высота равна средней линий , то диагонали будут взаимно перпендикулярны. Далее мы будем использовать этот факт . Тогда с одной стороны площадь трапеций равна
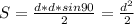$S=\frac{d*d*sin90}{2}=\frac{d^2}{2}$ , с другой стороны
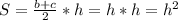$S=\frac{b+c}{2}*h=h*h=h^2$ из чего следует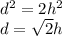 $d^2=2h^2\\
d=\sqrt{2}h$
Рассмотрим треугольник BCD

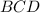радиус описанной около этого треугольника , будет равен радиусу описанного около трапеций ABCD

.
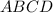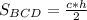Площадь треугольника $S_{BCD}=\frac{c*h}{2}$ , так как у нас центр окружности делить нашу высоту в отношений 3:4

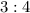(как вы сказали от большего) то обозначим соотношения как 3x;4x

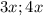. Тогда высота трапеций и треугольника будет равна h=7x

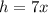. Значит площадь треугольника
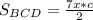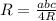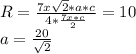$S_{BCD}=\frac{7x*c}{2}$ . Как известно по формуле $R=\frac{abc}{4R}$ вычислим наш радиус $R=\frac{7x\sqrt{2}*a*c}{4*\frac{7x*c}{2}}=10\\
a=\frac{20}{\sqrt{2}}$ . Теперь можно поступить так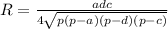
1) По теореме Пифагора выразим радиус , зная отношения
2) Выразим радиус по формуле $R=\frac{adc}{4\sqrt{p(p-a)(p-d)(p-c)}}$

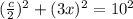
1) $(\frac{c}{2})^2+(3x)^2=10^2$
2) если все подставить перейдем на такое уравнение
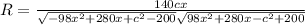$R=\frac{140cx}{\sqrt{-98x^2+280x+c^2-200}\sqrt{98x^2+280x-c^2+200}}$ оно равна 10

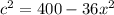1) $c^2=400-36x^2\\
$ подставляя во второе уравнение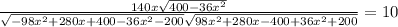
$\frac{140x\sqrt{400-36x^2}}{\sqrt{-98x^2+280x+400-36x^2-200}\sqrt{98x^2+280x-400+36x^2+200}}=10$
откуда решая это уравнение получаем
x=2

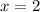тогда основание нижнее равна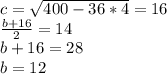
$c=\sqrt{400-36*4}=16\\
\frac{b+16}{2}=14\\
b+16=28\\
b=12$
ответ основания равны 16 и 12

4,4(54 оценок)

Ответ:

tonplaton

28.05.2022

Приступим. Найдем гипотенузу по теореме Пифагора.144+256=гипотенуза^2400=гипотенуза^2гипотенуза = 20смМедиана делит гипотенузу на 2 равные части, следовательно половина гипотенузы равна 10 смОпустим высоту из медианы и получим 2 подобных треугольника коэффициент подобия будет равен 2. Значит эта высота будет равна 12/2 = 6Найдем часть катета, которую отскла эта высота100-36=8^2Следовательно мы отсекли 8 смНаходим медиану, она будет гипотенузой.6^2+8^2=медиана^2медиана=10Эта задача с двумя решениями, потому что может поменять местами катетыНачало одинаковое, различия начинаются когда опускаем высоту. Пусть теперь нижний катет равен 12, тогда. Тогда будет коэффициент подобия треугольников тоже 2, но высота будет равна 16/2=8Найдем часть катета, которую отсекла высота. 100-64=6^2Следовательно мы отсекли 6см. Найдем медиану6^2+8^2=10^2медиана = 10см.Длина окружности - периметр круга.P=2nRD=2RR=5получается, что длина окружности равна 10n (n - пи, или 22/7)ответ: 10n

4,4(72 оценок)

Это интересно:

Стиль-и-уход-за-собой

29.07.2020

Как замаскировать прыщик с помощью зеленого консилера: советы и рекомендации...

Компьютеры-и-электроника

30.03.2020

Секреты изменения списка близких друзей Facebook на iPhone и iPad...

Компьютеры-и-электроника

04.03.2021

Как добавить фон на веб-страницу: простые шаги, которые помогут улучшить визуальное восприятие...

Стиль-и-уход-за-собой