Номер 1
<1=130 градусов
<3=<1=130 градусов,как вертикальные
<5=<3=130 градусов,как внутренние накрест лежащие
<1=<7=130 градусов,как внешние накрест лежащие
<5+<4=180 градусов,как односторонние
<4=180-130=50 градусов
<6=<4=50 градусов,как внутренние накрест лежащие
<8=<4=50 градусов,как соответственные
<2=<8=50 градусов,как внешние накрест лежащие
Номер 2
<2=(180-20):2=160:2=80 градусов
<1=80+20=100 градусов
<3=<1=100 градусов,как вертикальные
<3=5=100 градусов,как внутренние накрест лежащие
<5=<7=100 градусов,как вертикальные
<3+<6=180 градусов
<6=180-100=80 градусов
<4=<6=80 градусов,как внутренние накрест лежащие
<8=<4=80 градусов,как соответственные
Номер 3
<4=(180-110):2=70:2=35 градусов
<5=35+110=145 градусов
<8=<4=35 градусов,как соответственные
<1=<5=145 градусов,как соответственные
<6=<4=35 градусов,как внутренние накрест лежащие
<3=<5=145 градусов,как внутренние накрест лежащие
<2=<8=35 градусов,как внешние накрест лежащие
<7=<3=145 градусов,как соответственные
Номер 4
<2=<8,как накрест лежащие
Если при пересечении двух прямых третьей,накрест лежащие углы равны между собой,то прямые параллельны
а || b при секущей с
Объяснение:
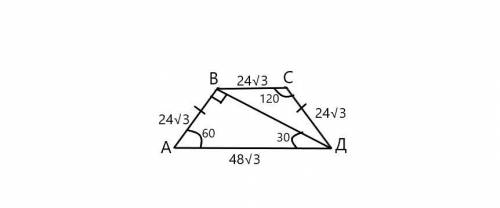
АВ=АД/2 (как катет лежащий против угла 30°) АВ=48√3/2=24√3; СД=АВ (трапеция равнобедренная); углы В и Д в треугольнике ВСД равны 30° (угол В в трапеции (180-60)=120°, угол В в треугольнике (120-90)=30°, угол Д в треугольнике (60-30)=30°); площадь трапеции равна сумме площадей треугольников АВД и ВСД; площадь треугольника равна половине произведения длин сторон на синус угла между ними.
S(АВД)=48√3*24√3*√3/4=864√3;
S(ВСД)=24√3*24√3*√3/4=432√3;
S(АВСД)=864√3+432√3=1296√3 ед².
Можно проще.
S(равнобедренной трапеции)=с*sinα(b-c*cosα), где b - основание , с - боковая сторона, α - угол при большем основании;
S=24√3*√3/2*(48√3-24√3/2)=36*36√3=1296√3 ед².
Еще можно через нахождение высоты, но думаю это лишнее.
Трапеция АВСD, AD II BC, AD > BC (ну, или равно, что совсем не интересно, потому что тогда ABCD квадрат). О - центр вписанной окружности.
ВО и АО - бисектриссы внутренних односторонних углов, поэтому они перпендикулярны. Треугольник АОВ прямоугольный. АВ^2 = AO^2 + BO^2;
Точно так же СD^2 = CO^2 + OD^2;
Остается сложить.