Так как вписан прямоугольный треугольник CKB угол CKB — прямой, а следовательно и угол AKB тоже прямой, так как они смежные.
CB=45 и AB=60 — катеты, AC — гипотенуза
По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы.
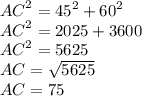
CK+KA=75
KA=CK+21
CK+(CK+21)=75
2CK=75-21
2CK=54
CK=27
KA=27+21=48
Найдем длину BK по той же теореме Пифагора:
CB²=CK²+BK²
BK²=CB²-CK²
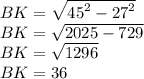
Найдем площадь треугольника AKB по формуле S=(ab)/2, где a и b катеты
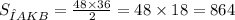
Теперь найдем площадь треугольника CKB:
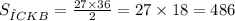
Отношение площадей треугольников AKB и CKB
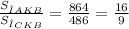
S(ΔAKB):S(ΔCKB) = 16:9
Если мы представим себя в роли наблюдателя, стоящего в начале координат и обращенного в сторону положительной полуоси х, то в случае а) ось у будет идти справа налево, а в случае б) — слева направо; В первом случае координатную систему называют правой, во втором левой.
Координаты точки C в новой и старой системе координат связаны соотношениями с учётом того, что они имеют разную ориентацию – старая система правая, а новая - левая:
{x'=(x-a)* cosφ + (y-b)*sinφ
{y'=(y-a)*sinφ - (y-b)*cosφ.
Для заданных условий: a = -3, b = -2, cosφ=-4/5, sinφ=√(1-(-4/5)^2 )=3/5.
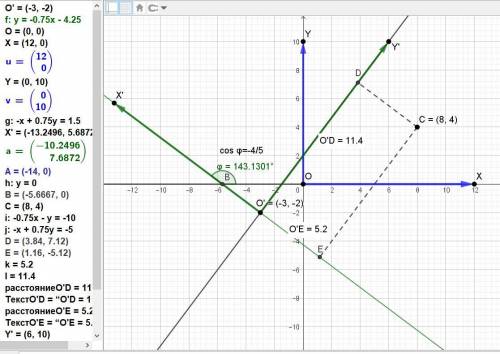
Проверим координаты точки С(8; 4) в новой (левой) системе.
x’ = (8-(-3))*(-4/5) + (4-(-2)*(3/5) = (-44/5) + (18/5) = -26/5 = -5,2.
y’ = (8-(-3))*(3/5) - (4-(-2)*(-4/5) = (33/5) - (-24/5) = 57/5 = 11,4.
На прилагаемом графике видно, что расчёт верен.
ответ: 5,6; 27,4см; 78°
Объяснение: для того, чтобы найти катеты в этом треугольнике, нужно гипотенузу умножить на синус и косинус угла 12°. Для нахождения второго острого угла надо от 90° вычесть угол 12°
один катет равен: 28*sin12°=28*0,2=5,6см
второй катет равен: 28/cos12°=28*0,98=27,4см
второй острый угол равен:90-12=78°