Люди с билетами! Дайте ответы БИЛЕТ №1
1. Свойство углов при основании равнобедренного треугольника
2. Высота, биссектриса, медиана треугольника (определения).
3. Задача по теме " Соотношения между сторонами и углами
треугольника".
БИЛЕТ №2
1. Теорема о сумме углов треугольника
2. Взаимное расположение двух прямых.
Основное свойство параллельных прямых.
3. Задачи по теме «Равнобедренный треугольник».
БИЛЕТ №3
1. Теорема о биссектрисе равнобедренного треугольника
2. Треугольник (определение). Равные треугольники. Существование треугольника, равного данному.
3. Задачи по теме «Параллельные прямые».
БИЛЕТ №4
1. Признак параллельности прямых (доказательство для случая равенства накрест лежащих углов).
2. Прямоугольный треугольник. Признаки равенства прямоугольных треугольников
3. Задачи по теме «Смежные и вертикальные углы»
БИЛЕТ №5
1. Признак параллельности прямых (доказательство для случая равенства соответствующих углов)
2. Окружность (определение). Радиус, хорда, диаметр окружности.
3. Задачи по теме «Окружность».
БИЛЕТ №6
1. Признак параллельности прямых (доказательство для случая суммы односторонних углов)
2. Касательная к окружности. Взаимное расположение двух окружностей.
3. Задачи по теме " Высота, медиана и биссектриса треугольника".
БИЛЕТ №7
1. Теорема о накрест лежащих углах, образованных при пересечении двух параллельных прямых третьей.
2. Перпендикулярные прямые (определение). Перпендикуляр к прямой.
3. Задачи по теме "Внутренние и внешние углы треугольника ".
БИЛЕТ №8
1. Теорема о сумме односторонних углах, образованных при пересечении двух параллельных прямых третьей.
2. Расстояние от точки до прямой. Расстояние между параллельными прямыми.
3. Задачи по теме «Смежные и вертикальные углы»
БИЛЕТ №9
1. Теорема о соответственных углах, образованных при пересечении двух параллельных прямых третьей
2. Прямоугольный треугольник (определение). Катет. Гипотенуза. Свойства прямоугольного треугольника.
3. Задачи по теме «Равнобедренный треугольник»
БИЛЕТ №10
1. Признак равенства треугольников по двум сторонам и углу между ними.
2. Теорема о диаметре, перпендикулярного хорде.
3. Задачи по теме «Параллельные прямые».
БИЛЕТ №11
1. Признак равенства треугольников по стороне и двум прилежащим к ней углам.
2. Теоремы и доказательства. Аксиомы. Приведите примеры.
3. Задачи по теме «Сумма углов треугольника»
БИЛЕТ №12
1. Признак равенства треугольников по трем сторонам.
2. Окружность, описанная около треугольника (определение). Теорема о центре окружности, описанной около треугольника.
3. Задачи по теме "Окружность и ее элементы".
БИЛЕТ №13
1. Теорема об отрезках касательной.
2. Построение биссектрисы угла.
3. Задача по теме «Равнобедренный треугольник».
БИЛЕТ №14
1. Теорема о соотношении между сторонами и углами треугольника.
2. Построение треугольника по двум сторонам и углу между ними
3. Задача по теме «Окружность»
БИЛЕТ №15
1. Построить угол равный данному.
2. Наклонная, проведенная из данной точки к прямой, расстояние от точки до прямой.
3. Задача по теме «Признаки равенства треугольников»
БИЛЕТ №16
1. Свойство смежных углов.
2. Неравенство треугольника.
3. Задача по теме «Прямоугольные треугольники».
БИЛЕТ №17
1. Свойство вертикальных углов.
2. Окружность, вписанная в треугольник (определение). Теорема о центре окружности, вписанной в треугольник.
3. Задача по теме «Признаки равенства треугольников»
БИЛЕТ №18
1. Деление отрезка пополам
2. Внешний угол треугольника (определение). Теорема о внешнем угле треугольника.
3. Задача по теме «Равнобедренный треугольник»
БИЛЕТ №19
1. Наклонная, проведенная из данной точки к прямой, расстояние от точки до прямой.
2. Теорема о свойстве катета, лежащего против угла в 30º.
3.Задача по теме «Сумма углов треугольника»
БИЛЕТ №20
1. Теорема о внешнем угле треугольника
2. Признаки равнобедренного треугольника.
3. Задача по теме «Окружность».

👇

Увидеть ответ

Ответ:

Алеся1111115

27.07.2022

1) углы при основании равнобедренного треугольника равны.

2) Высота- это перпендикуляр опущенный с вершины на противоположную сторону.

Биссектриса- луч, исходящий из вершины угла и делящий его пополам.

Медиана- отрезок соединяющий вершину с серединой противоположной стороны.

3. Что за задача?

4,8(92 оценок)

Открыть все ответы

Ответ:

kushkulina2011

27.07.2022

Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство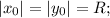 |x_0|=|y_0|=R; учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) x_0=-y_0=R

уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2

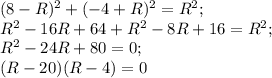$(8-R)^2+(-4+R)^2=R^2;\\ R^2-16R+64+R^2-8R+16=R^2;\\ R^2-24R+80=0;\\ (R-20)(R-4)=0$ ;

R=20 или R=4

значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат

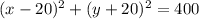
(x-20)^2+(y+20)^2=400

и 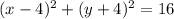(x-4)^2+(y+4)^2=16

вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр

Ищем координаты середины отрезка АВ,

$x=\frac{-2+2}{2}=0; y=\frac{3+1}{2}=2;$

(0;2)

ищем уравнение пряммой АВ в виде y=kx+b

3=-2k+b;

1=2k+b;

2=-4k

1=2k+b;

k=-0.5

b=2;

y=-0.5x+2

перпендикулярные пряммые связаны соотношением угловых коэффициентов

k_1k_2=-1

поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2

учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде

y=kx+b (k=2)

2=2*0+b;

b=2

y=2x+2 или y-2x-2=0

в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили

4,4(91 оценок)

Ответ:

Сандалёк

27.07.2022

∠ EBD = 6,4°.

Объяснение:

Дан угол FAC, вписанный в окружность, и отношения этого угла к шести другим углам, вписанным в ту же окружность. Эти семь углов дают нам 7 дуг, на которые опираются данные 7 углов: AD, BE, CF, DG, EA, FB и GC.

Так как угол FAC вдвое меньше угла ACE, то и дуга CF (на которую опирается угол FAC) вдвое меньше дуги EA (на которую опирается угол ACE). Обозначив CF за х, получим равенство для дуги EA:

2х=EA.

Аналогичным образом получаем выражения для других дуг

3х=GC

4х=BE

5х=DG

6х=FB

7х=AD

Итак, мы имеем 7 дуг (AD, BE, CF, DG, EA, FB и GC), и 6 из них мы выразили через дугу CF, которую обозначили х.

Пройдя по дугам в таком порядке: AD, DG, GC, CF, FB, BE, EA, мы опишем окружность трижды. Сумма градусных мер дуг окружности, образующих полную окружность, равна 360° . Так как мы описали окружность трижды, то сумма наших семи дуг равна 3*360° =1080°.

Поскольку в самом начале мы выразили 6 дуг через одну, составляем уравнение: х+2х+3х+4х+5х+6х+7х = 1080°

28х = 1080

х = 1080:28 = 38,57°

Итак, градусная мера дуги CF равна 38,57°

Угол EBD, который нужно найти, опирается на дугу DE.

Дуги DE, EA и AD образуют полную окружность и дают в сумме 360° .

Так как EA = 2х и AD = 7х, в сумме они дадут 9х, то есть 9 градусных мер дуги CF. 9*38,57° = 347,14°

Находим дугу DE: 360° - 347,14° = 12,86°.

Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается, значит градусная мера угла EBD равна половине градусной меры дуги DE:

12,86°:2 = 6,43°.

4,4(20 оценок)

Это интересно:

Кулинария-и-гостеприимство

03.04.2023

Узнай, как сделать невероятно вкусный и загадочный мартини драгон...

Здоровье

20.07.2020

Симптомы СРК: как безопасно путешествовать?...

Образование-и-коммуникации

18.12.2022

Основные принципы подготовки к экзамену без зубрежки...