Объяснение:
Дано:
Точка A:
Xa = 2;
Ya = -3.
Точка B:
Xв = -4;
Yв = 1.
Точка C:
Xc = -3;
Yc = -2.
Находим:
а)
Координаты вектора АВ:
AB = {Xв-Xa; Yв-Ya} = {-4-2; 1-(-3)} = { -6; 4}
б)
Координаты середины отрезка BC:
Xм = (Хв + Хс)/2 = (-4 -3)/2 = -7/2
Yм = (Yв + Yс)/2 = (1 - 2)/2 = -1/2
в) Расстояние между точками А и В
d = √ ( (-6)² + 4²) = √ (36+16) = √52 = 2*√13
2.
Чтобы найти координаты точки пересечения прямых, необходимо решить систему уравнений:
8x+6y=12
6x+3y=12
Умножим обе части второго уравнения на 2:
8x+6y=12
12x+6y=24
Вычтем из второго уравнения первое:
4х = 12
x = 3
y = -2
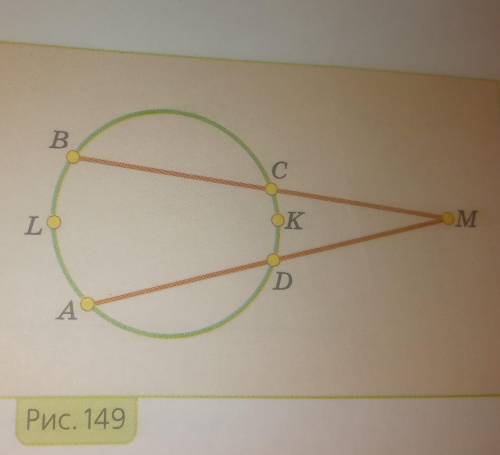
Объяснение:
Соединим А и В, С и D. Четырехугольник ABCD - вписанный, значит <ABC+<ADC=180° и <CDM+<ADC=180°, значит <ABC=<CDM. Аналогично <BAD=<DCM.
Из тр-ка △CMD <CMD(AMB)=180-<CDM-<DCM=180-<ABC-<BAD
<ABC=1/2*(AD+CD); <BAD=1/2(BC+CD).
<AMB=180-1/2*(AD+CD)-1/2*(BC+CD)=180-1/2*(AD+CD+BC)-1/2*CD
Для дуг окружности можно записать:
AD+CD+BC=360-AB - подставим в последнее выражение:
<AMB=180-1/2*(360-АВ)-1/2*СD=180-180+1/2*АВ-1/2*СD=1/2*(AB-CD)=1/2*(ALB-CKD)