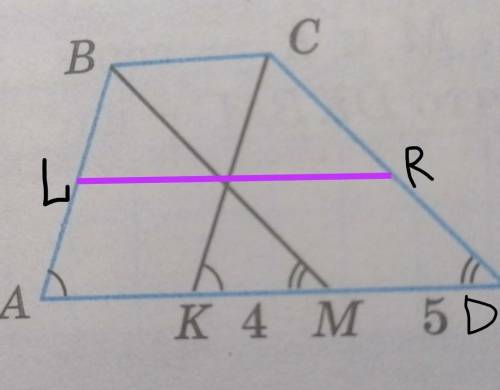
Пусть LR – средняя линия трапеции ABCD
Угол CDA=угол BMA по условию, тогда прямые CD u BM – паралельны, а углы CDA и BMA – соответственные при параллельных прямых CD u BM и секущей AD.
ВС//AD (так как основания трапеции параллельны) => ВС//MD
Исходя из найденного: BCDM – параллелограмм, так как его стороны попарно параллельны.
Следовательно ВС=MD=5 так как противоположные стороны параллелограмма равны.
Угол BAD=угол CKD по условию, тогда прямые BA u CK – паралельны, а углы BAD и CKD – соответственные при параллельных прямых ВА u СК и секущей AD.
ВС//AD (так как основания трапеции параллельны) => ВС//AK
Исходя из найденного: BCKA – параллелограмм, так как его стороны попарно параллельны.
Следовательно AK=ВС=5 так как противоположные стороны параллелограмма равны.
Средняя линия трапеции равна полусумме оснований.
Тоесть LR=(BC+AD)÷2
BC=5 (найдено ранее);
АD=AK+KM+MD=5+4+5=14
Тогда LR=(5+14)÷2=9,5
ответ: 9,5
Боковые грани одинаково наклонены к плоскости основания - высота падает в центр вписанной окружности основания.
Площадь основания по формуле Герона
p=15 (полупериметр)
S =√(p(p-a)(p-b)(p-c)) =√(15*8*5*2) =20√3
S=pr => r =20√3/15 =4/√3 =OH
По теореме о трех перпендикулярах
SO⊥(ABC), OH⊥AB (радиус в точку касания) => SH⊥AB
Угол между плоскостями - угол между перпендикулярами к общей прямой.
∠SHO - линейный угол двугранного угла SABC
tg(SHO) =SO/OH =√3 => ∠SHO=60°