1. S = 25,5 дм².
2. Cosα = 0,96.
Объяснение:
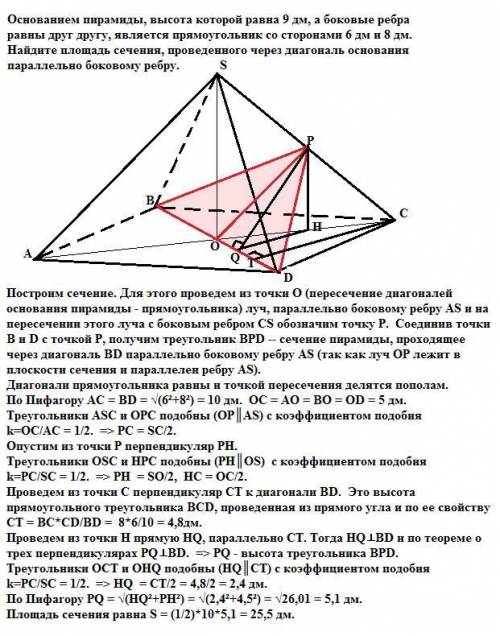
1. Построим сечение. Для этого проведем из точки О (пересечение диагоналей основания пирамиды - прямоугольника) луч, параллельно боковому ребру AS и на пересечении этого луча с боковым ребром CS обозначим точку Р. Соединив точки В и D с точкой Р, получим треугольник BPD -- сечение пирамиды, проходящее через диагональ BD параллельно боковому ребру AS (так как луч ОР лежит в плоскости сечения и параллелен ребру AS).
Диагонали прямоугольника равны и точкой пересечения делятся пополам.
По Пифагору АС = BD = √(6²+8²) = 10 дм. ОС = АО = BO = OD = 5 дм.
Треугольники ASC и OPC подобны (OP║AS) c коэффициентом подобия k=OC/AC = 1/2. => PC = SC/2.
Опустим из точки Р перпендикуляр РН.
Треугольники OSC и HPC подобны (PH║OS) c коэффициентом подобия k=PC/SC = 1/2. => PH = SO/2, НС = ОС/2.
Проведем из точки С перпендикуляр СТ к диагонали BD. Это высота прямоугольного треугольника BCD, проведенная из прямого угла и по ее свойству CТ = BC*CD/BD = 8*6/10 = 4,8дм.
Проведем из точки Н прямую HQ, параллельно СТ. Тогда HQ⊥BD и по теореме о трех перпендикулярах PQ⊥BD и является высотой треугольника BPD.
Треугольники OCТ и OHQ подобны (HQ║CT) c коэффициентом подобия k=PC/SC = 1/2. => HQ = CT/2 = 4,8/2 = 2,4 дм.
По Пифагору PQ = √(HQ²+PH²) = √(2,4²+4,5²) = √26,01 = 5,1 дм.
Площадь сечения равна S = (1/2)*10*5,1 = 25,5 дм².
2. Определение: Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек. АВ1 и СD1 скрещивающиеся прямые по определению.
Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся.
Проведем диагональ А1В грани АА1В1В. A1B параллельна СD1 как соответствующие диагонали противоположных граней параллелепипеда. АВ1 и А1В - скрещивающиеся прямые. Следовательно, искомый угол - это угол между прямыми АВ1 и А1В. Боковая грань АА1В1В - прямоугольникб диагонали которого пересекаются в точке О и этой точкой делятся пополам. Диагонали равны между собой и по Пифагору равны √(АА1²+АВ²) = √(6²+8²) = 10 ед. Тогда АО = А1О = 5 ед. АА1 = 6 ед. (дано).
Найдем косинус этого угла по теореме косинусов:
Cosα = (AO²+A1O² - AA1²)/(2*AO*AO) = (5²+5²-6²)/(2*25) = 14/50 = 0,28.
Тогда по известной формуле
Sinα = √(1 - Cos²α) = √(0,9216) = 0,96.
Объяснение:
К середине XIX века были открыты 63 химических элемента, и попытки найти закономерности в этом наборе предпринимались неоднократно. В 1829 году Иоганн Дёберейнер опубликовал найденный им «закон триад»: атомная масса многих элементов близка к среднему арифметическому двух других элементов, близких к исходному по химическим свойствам (стронций, кальций и барий; хлор, бром и иод и др.). Первую попытку расположить элементы в порядке возрастания атомных весов предпринял Александр Эмиль Шанкуртуа (1862), который создал «Теллуров винт», разместив элементы на винтовой линии, и отметил частое циклическое повторение химических свойств по вертикали. Эти модели не привлекли внимания научной общественности.
В 1866 году свой вариант периодической системы предложил химик и музыкант Джон Александр Ньюлендс, модель которого («закон октав») внешне немного напоминала менделеевскую, но была скомпрометирована настойчивыми попытками автора найти в таблице мистическую музыкальную гармонию. В этом же десятилетии было предпринято ещё несколько попыток систематизации химических элементов, и ближе всего к окончательному варианту подошёл Юлиус Лотар Мейер (1864). Однако главное отличие его модели заключалось в том, что за основу периодичности была взята валентность, которая не является единственной и постоянной для отдельно взятого элемента, и поэтому такая таблица не могла претендовать на полноценное описание физики элементов и не отражала периодического закона.
Д. И. Менделеев. Рукопись «Опыта системы элементов, основанной на их атомном весе и химическом сходстве». 17 февраля 1869 года (1 марта 1869 года)
Д. И. Менделеев опубликовал свою первую схему периодической таблицы в 1869 году в статье «Соотношение свойств с атомным весом элементов» ( журнал Русского химического общества); ещё ранее (февраль 1869 года) научное извещение об открытии было разослано Менделеевым ведущим химикам мира. Прообразом периодической системы элементов стала таблица, составленная Менделеевым 17 февраля 1869 года (1 марта 1869 года) и озаглавленная «Опыт системы элементов, основанной на их атомном весе и химическом сходстве»[2]. И только в декабре выходит работа немецкого химика Мейера, который изменил своё решение в пользу мысли Д. И. Менделеева и в зарубежной литературе считается либо «одним из первооткрывателей», либо «независимо от Менделеева опубликовавшим этот периодический закон». Однако Л. Мейер в своих исследованиях не пошёл дальше расстановки части (28 из 63) открытых на тот момент элементов в сплошной ряд и периодического закона не формулировал вообще, в то время как Д. И. Менделеев в своей таблице оставил несколько свободных мест и предсказал ряд фундаментальных свойств ещё не открытых элементов и само их существование, а также свойства их соединений (экабор, экаалюминий, экасилиций, экамарганец — соответственно, скандий, галлий, германий, технеций). Некоторые элементы, а именно, бериллий, индий, уран, торий, церий, титан, иттрий, имели на момент работы Менделеева над периодическим законом неправильно определённый атомный вес, и поэтому Менделеев исправил их атомные веса на основании открытого им закона. Этого не могли сделать ни Деберейнер, ни Мейер, ни Ньюлендс, ни де Шанкуртуа.
Д. И. Менделеев. Портрет работы Ильи Репина (1885)
По легенде, мысль о системе химических элементов пришла к Менделееву во сне, однако известно, что однажды на во как он открыл периодическую систему, учёный ответил: «Я над ней, может быть, двадцать лет думал, а вы думаете: сидел и вдруг… готово»[3].