Смотрите рисунок. Продолжим стороны АВ и ДС до их пересечения между собой получим точку М. Поскольку биссектриса <А перпендикулярна СД, то она – биссектриса перпендикулярна и ДМ. Следовательно, треугольник АДМ - равнобедренный. И АД = АМ. Впрочем, это не важно. Но раз треугольник АДМ равнобедренный, а АЕ перпендикуляр на ДМ, то ДЕ = МЕ = 5. Тогда МС = МЕ-СЕ = 5 – 1 = 4. Следовательно, МД = МС + СЕ + ЕД = 4 + 1 + 5 = 10. Поскольку АД и ВС параллельны между собой, то треугольники ВМС и АМД - подобны. Из подобия этих треугольников вытекает, что АД/ВС = МД/МС = 10/4 = 5/2
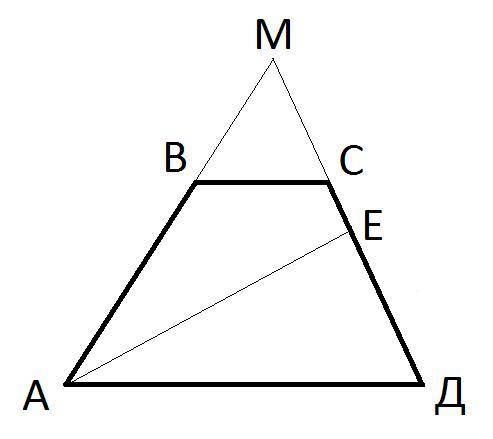
Что по условию надо найти не понятно
Объяснение:
<САВ=<СВА=(180-<С)/2=(180-60)/2=60 т к тр-к
равнобедренный В тр-ке
<САВ=<СВА=<АСВ=60 значит тр-к АВС равносторонний.
<КАВ=1/2×<САВ=1/2×60=30,т к АК биссектриса
<АКС=90,т к в равностороннем тр-ке
биссектриса является высотой