15 = 45 - угол НСВ; угол НСВ = 30 градусов; угол НСВ = угол САВ; ВС = АВ/2 = 6
Что-то мне подсказывает, что угол НСВ = угол САВ. Что-то вроде подобия треугольников Что-то мне подсказывает, что угол КСВ = 45 градусов, уж не определение биссектрисы ли? (Ли - известный китайский ученый, придумал биссектрису ли). И что-то мне подсказывает, что если от 45 отнять 15, то получится 30.
Есть нечто сакраментальное (сакрально-ментальное, то есть тайнодуховное, а может, и чакра-ментальное...) в том, что точка К лежит ближе к А, чем Н. Не знаю, правы ли космические силы, но говорят они мне, что обозначил правильно вершины треугольника я и вычислил угол против катета СВ, 30 равный градусам.
В прямоугольном треугольнике же катет, против угла 30 градусов лежащий, равен гипотенузной половине, в сантиметрах выраженной.
Ну, отметил :))) бывает :)))
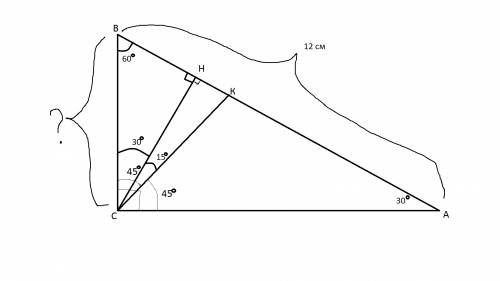
Так как СК - биссектриса угла АСВ, то угол ВСК = углу КСА = 45 градусов.
При этом угол ВСК равен сумме углов ВСН и НСК. Известно, что угол НСК равен 15 градусам. Следовательно, угол ВСН=уголВСК-уголНСК= 45-15=30 градусов.
Так как угол ВНС прямой (СН высота треугольника АСВ), то по сумме углов треугольника СВН, угол СВН= 180-90-30=60 градусов.
Угол ВАС треугольника АВС в соответсвии с этим равен 180-90-60=30 градусов.
По свойству прямоугольного треугольника, в котором напротив угла, равного 30 градусов лежит катет, длина которого равна половине длины гипотенузы.
Следовательно, ВС=½АВ=6 см.
ответ: ВС=6 см
Объяснение:
ΔDBC-равнобедренный(тк ∠В=45°, а ∠D=90°)
пусть х-сторона BD и DC(так как они равны)
BC²=BD²+DC²
36=x²+x²
36=2х²
отсюда х=3√2
ΔABD-прямоугольный, так как∠А равен 30°, и катет, лежащий напротив угла в 30°, равен половине гипотенузы, то АВ=6√2 см
по теореме Пифагора AD=\sqrt{ AB^{2}- BD^{2} }
AB
2
−BD
2
=\sqrt{72-18}= \sqrt{54}=3 \sqrt{6}
72−18
=
54
=3
6
AC=AD+DC=3√2+3√6=3(√2+√6) cм