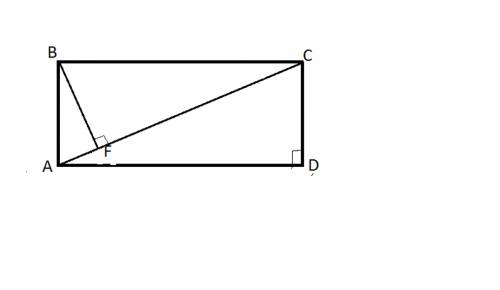
В прямоугольнике ABCD AC диагональ, BF перпендикулярно AC.
Доказать, что треугольник ABF подобен треугольнику CAD
Доказательство 1)
Рассмотрим треугольники АСD и АСF. Оба они прямоугольные.
Стороны АВ и СD параллельны как стороны прямоугольника, и АС - секущая при них. Углы ВАF и АСD- накрестлежащие и потому равны.
Прямоугольные треугольники, имеющие равный острый угол, подобны.
Доказательство 2)
ВF перпендикулярна АС, следовательно, является высотой прямоугольного треугольника АВС.
Высота прямоугольного треугольника делит его на взаимно подобные треугольники:
АВF~ BFC~ ABC.
Но треугольник АВС равен треугольнику АСD, следовательно, треугольник ABF подобен треугольнику CAD.
№2. чтобы доказать что треугольник равносторонний, надо доказать что трекгольники ABC, CDE,AEF равны.
док-жем что ABC, CDE,AEF равны:
AB=CD=EF(по усл)
BC=DE=FA(по усл)
угол B= углу D=углу E(по усл), тогда треуг ABC=CDE=AEF
ABC=CDE=AEF соответственно равны, тогда AC=CE=AE,тогда треуг ACE равносторонний
№3. док-то что треуг AOD=треуг CBO
AO=CO( по усл)
DO=BO(равные остатки отрезков AB=СD)
уг COB=уг AOD( вертик угла)
треуг AOD=треуг CBO, тогда все соотв элементы равны, тогда уг ABC=ADC, а BAD=BCD.