В треугольнике ABC ∠С = 90°, AB = 5, tgA = 7/24. Найдите AC.
===========================================================
▪Первый теорема Пифагора ):tgA = BC/AC = 7/24Пусть ВС = 7х, АС = 24х, тогда Применим теорему Пифагора:АС² + ВС² = АВ²( 24х )² + ( 7х )² = 5²576х² + 49х² = 25625х² = 25х² = 1/25 ⇒ х = 1/5 = 0,2 Значит, АС = 24х = 24•0,2 = 4,8▪Второй Тригонометрия ):tg²A + 1 = 1/cos²Acos²A = 1/( tg²A + 1 ) = 1/( (7/24)² + 1 ) = 1/( 625/576 ) = 576/625cosA = ± 24/25 ⇒ ∠A - острый ⇒ cosA = 24/25cosA = AC/AB = 24/25 ⇒ AC = ( 5 • 24 )/25 = 24/5 = 4,8ОТВЕТ: 4,8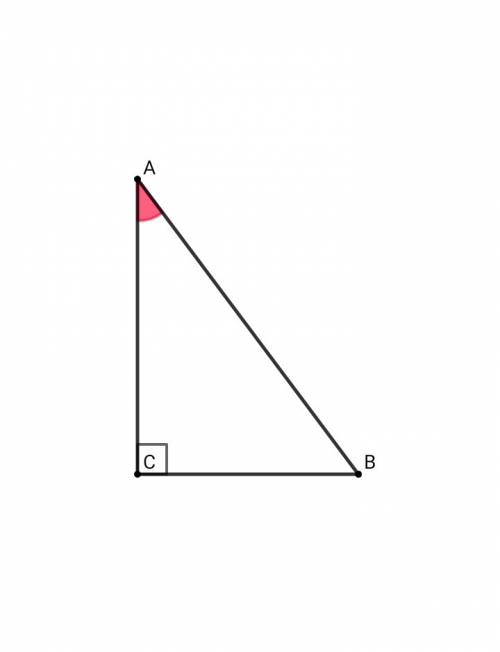
Сумма углов выпуклого
Так как углы выпуклого двенадцатиугольника пропорциональны числам 7,10,2,10,5,4,2,4,5,3,3,5, то обозначив градусную меру первого через 7х градусов, сооственно в градусах градусные меры остальных будут
10х,2х,10х,5х,4х,2х,4х,5х,3х,3х,5х.
Дальше составляем уравнение
7х+10х+2х+10х+5х+4х+2х+4х+5х+3х+3х+5х=1800
60х=1800
х=30 градусов
соотвественно умножив на соотвествующий коэфициент находим углы
210 градусов, 300 градусов, 60 градусов, 300 градусов, 150 градусов, 120 градусов, 60 градусов, 120 градусов, 150 градусов, 90 градусов, 90 градусов, 150 градусов