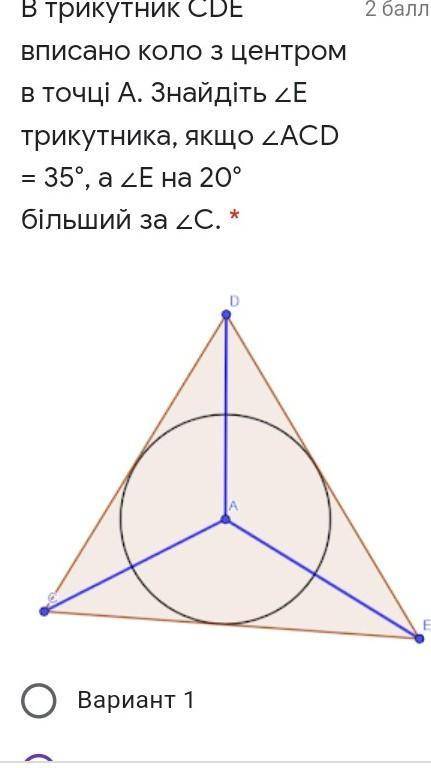
ответ:д) 80°
Объяснение:
Центр вписанного кола такою i центр перетину бiсектрис. Якщо АСD =30°, тодi кут C = 30*2=60° Кут Е на 20 бiльше, тому кут Е = 60+20=80°
1.
P(4;3), T(-2;5).
Используем уравнение прямой, проходящей через две точки.
Если даны две точки A(x₁; y₁) и B(x₂; y₂), тогда уравнение прямой, проходящей через эти две точки будет
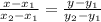
То есть у нас даны две точки P(4;3) и T(-2;5), уравнение прямой, проходящей через них будет

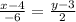
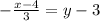
-(x-4) = 3·(y-3),
4 - x = 3y - 9,
3y + x - 9 - 4 = 0,
x + 3y - 13 = 0.
Можно сделать проверку: подставим координаты каждой точки в уравнение и проверим выполнение равенства.
P(4;3):
4 + 3·3 - 13 = 4 + 9 - 13 = 0. Верно.
T(-2;5):
(-2) + 3·5 - 13 = -2 + 15 - 13 = 0. Верно.
ответ. x + 3y - 13 = 0.
2.
x + 3y - 13 = 0,
Уравнение оси Ox (оси абсцисс): y = 0. Подставим это в уравнение прямой и получим x + 3·0 - 13 = 0, ⇔ x = 13.
Итак, пересечение прямой с осью Ox дает точку (13;0).
Уравнение оси Oy (оси ординат): x = 0. Подставим это в уравнение прямой и получим 0 + 3y - 13 = 0, ⇔ 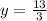 .
.
Итак, пересечение прямой с осью Oy в точке 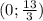 .
.
3.
Дана прямая x - y + 2 = 0 и окружность (x-2)² + (y-1)² = 9.
Чтобы найти координаты точек пересечения решим систему двух уравнений на два неизвестных.
Из уравнения прямой находим y = x+2, подставим это в уравнение окружности: (x-2)² + ( x+2 - 1)² = 9,
(x-2)² + (x+1)² = 9,
x² - 4x + 4 + x² + 2x + 1 = 9,
2x² - 2x + 5 - 9 = 0,
2x² - 2x - 4 = 0,
x² - x - 2 = 0,
D = (-1)² - 4·1·(-2) = 1 + 8 = 9 = 3²,
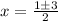
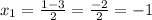
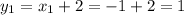
Итак, координаты первой точки (-1; 1).
 .
.
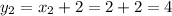
Итак, координаты второй точки (2; 4).
ответ. (-1; 1), (2; 4).
№ 4 - ответ: а = 3√5; b = 6√5
№ 5 - ответ: высота равна 2 см; углы треугольника : 30°, 30°, 120°.
Объяснение:
№ 4.
Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, является средней пропорциональной величиной между отрезками, на которые основание перпендикуляра делит гипотенузу.
Если х - длина перпендикуляра, то:
х = √ (3 · 12) = √ 36 = 6 см.
По теореме Пифагора находим катеты:
а = √(3² + 6²) = √(9+36) = √45 √9·5= 3√5
b = √(12² + 6²) = √(144+36) = √180 = √36·5 = 6√5
ответ: а = 3√5; b = 6√5
№ 5
1) По теореме Пифагора находим высоту:
h = √[(4² - ((4√3)/2)²] = √ [16 - (2√3)²] = √ (16 - 4· 3) = √4 = 2 см,
где 4√3)/2 - это половина длины основания, т.к. в равнобедренном треугольнике высота, опущенная на основание, делит его пополам;
2) Высота равна 2 см, а боковая сторона равна 4 см. Значит, высота лежит против угла 30°, т.к. катет, лежащий против угла 30°, равен половине гипотенузы.
Так как треугольник равнобедренный, то и второй угол (при основании) также равен 30°.
Находим 3-й угол:
180 (сумма внутренний углов треугольника) - 30 - 30 = 120°.
ответ: высота равна 2 см; углы треугольника : 30°, 30°, 120°.
ответ: в) 90°
Объяснение: фото смотри