Объяснение:
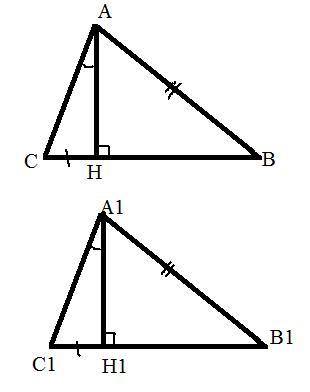
Дано: AB = A1B1, CH=C1H1, <CAH=<C1A1Н1. АН, А1Н1 - высоты.
Доказать: △АВС=△А1В1С1.
Док-во:
Рассмотрим △АСН и △А1С1Н1. Они прямоугольные и у них CH=C1H1 - катеты, <CAH=<C1A1Н1 - острые углы. Значит △АСН=△А1С1Н1 по 4 признаку (по катету и острому углу). => АС=А1С1, АН=А1Н1.
Рассмотрим △АВН и △А1В1Н1. Они прямоугольные и у них АН=А1Н1 - катеты, AB = A1B1 - гипотенузы. Значит △АВН=△А1В1Н1 по 2 признаку (по катету и гипотенузе). => ВН=В1Н1.
CH=C1H1, ВН=В1Н1, CB=CH+HB, C1B1=C1H1+H1B1 => CB=C1B1.
Таким образом для треугольников △АВС и △А1В1С1 имеем, что AB = A1B1, АС=А1С1, CB=C1B1, значит △АВС=△А1В1С1 по 3му признаку (по 3м сторонам), чтд.
Надо воспользоваться формулой: sin(2α) = 2*sin(α)*cos(α).
Функцию sin(α) выразим через cos(α).
sin(α) = √(1 - cos²(α)).
Подставим в первое уравнение:
-3/5 = 2*√(1 - cos²(α))*cos(α). Возведём обе части в квадрат.
9/25 = 4*(1 - cos²(α))*cos²(α). Приведём к общему знаменателю и раскроем скобки.
9 = 100cos²(α)) - 100cos^4(α).
Получили биквадратное уравнение. Введём замену: cos²(α) = t.
Тогда уравнение имеет вид: 100t² - 100t + 9 = 0.
Ищем дискриминант:
D=(-100)^2-4*100*9=10000-4*100*9=10000-400*9=10000-3600=6400;
Дискриминант больше 0, уравнение имеет 2 корня:
t_1=(√6400-(-100))/(2*100)=(80-(-100))/(2*100)=(80+100)/(2*100)=180/(2*100)=180/200=0,9;
t_2=(-√6400-(-100))/(2*100)=(-80-(-100))/(2*100)=(-80+100)/(2*100)=20/(2*100)=20/200=0,1.
Обратная замена: cos(α) = ±√t.
cos(α1,2) = ±√0,9 ≈ ±0,94868.
cos(α3,4) = ±√0,1 ≈ ±0,31623.
Данным косинусам соответствуют углы:
(α1,2) = 18,43495 и 161,5651 градусов,
(α3,4) = 71,5651 и 108,43495 градусов.
По заданию угол должен быть в промежутке (90° < α < 135°).
ответ: cos α = -√0,1 ≈ -0,31623.
ты и я ты и я мы с тобой друзьяяя да ты и я ты и ч мы с тобой доузьяяч