Площадь ромба равна 120 см², а одна из диагоналей больше другой на 14 см. Найдите длину неизвестной диагонали.
▔ ▔ ▔
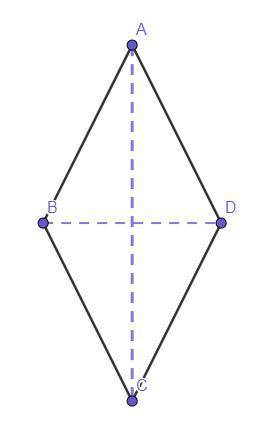
★☆★ Чертёж смотрите во вложении ★☆★
Дано:Четырёхугольник ABCD — ромб.
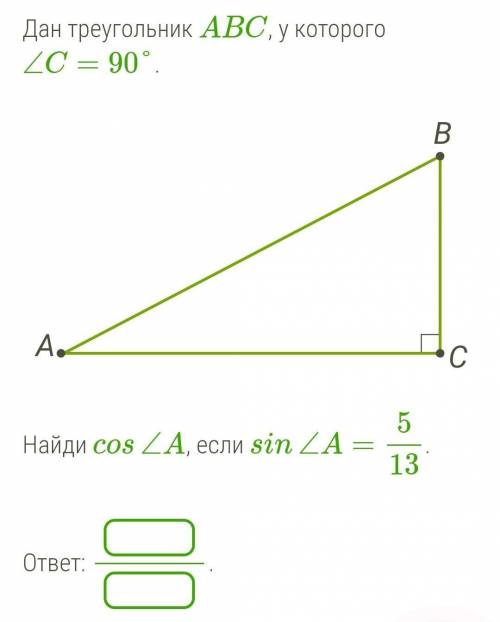
S(ABCD) = 120 см².
AC и BD — диагонали.
АС = BD+14 см.
Найти:BD = ?
Решение:Пусть BD = х.
Тогда —
АС = х+14 см.
▸Площадь ромба равна половине произведения его диагоналей◂
То есть —
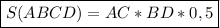
Подставим в формулу известные нам значения —
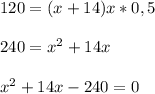
Решаем полученное квадратное уравнение —
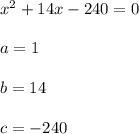
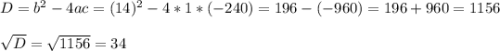
Ищем корни —
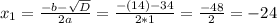
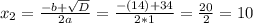
Как видим, корень х₁ не подходит, так как длина отрезка не может выражаться отрицательным числом.
Поэтому, BD = х = 10 см.
ответ:10 см.
![\sqrt[n]{x}](/tpl/images/0258/0436/b773b.png)
12/13
Объяснение:
sin²A+cos²A=1
cosA=√(1+sin²A)=√(1-(5/13)²)=
√(169/169-25/169)=√(144/169)=12/13