ответ: 8 см²
Объяснение:
КАК решают такие задачи.
Часто подобные задачи решаются вычитания ( или сложения ) площади фигур, образованных клетками. Чертят прямоугольник, который описывает данную фигуру. Вычисляют его площадь, затем площадь "лишних"фигур ( обычно это треугольники) и вычитают. Остается искомая площадь . Или делят данную фигуру на части, у которых удобно найти площадь, и затем складывают.
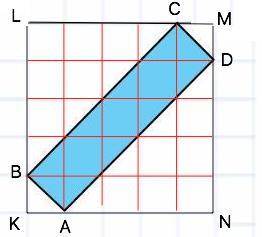
Обозначим прямоугольник АВСD, опишем около него прямоугольник KLMN. (см. вложение).
S(KLMN)=KL•LM=5•5=25 см²
∆BLC=∆AND по равным катетам.
Их общая площадь Ѕ₁=4•4=16 см²
∆BKA=∆CMD по равным катетам. Их общая площадь
Ѕ₂=1•1=1 см²⇒
Ѕ (ABCD)=S (KLMN)- 16-1=8 см²
----------
Другой
Из ∆ (BLC) по т.Пифагора найдем длину ВС=√(4²+4²)=4√2 см.
Из ∆ (ВКС) по т.Пифагора найдем ширину АВ=√(1²+1²)=√2 см
Площадь прямоугольника равна произведению его длины на ширину:
S(ABCD)=ВС•АВ=4√2•√2=8 см²
1) Так как угол MNO = 60°, а стороны MO=ON как радиусы, то треугольник MNO - равнобедренный и углы OMN и MNO равны друг другу (60°)
В сумме эти углы дают 120°, значит третий угол MON будет равен 180°-120° = 60°. Значит треугольник MON - разносторонний и сторона MN равна радиусу. Диаметр равен двум радиусам:
D=2R=2MN=2*5,4=10,8см
2) Угол MNR равен сумме углов MNO и ONR , то есть: 60° + 90° = 150°
3) Аналогично рассмотрим треугольник OKL , так как KL = MN , то точно так же треугольник OKL является равносторонним, а значит все его углы равны по 60° => угол OKL = углу NKL = 60°
4
Объяснение:
Сумма внутренних углов выпуклого многоугольника = 180°(n-2), а сумма внешних углов = 180° -<а1 + 180° -<а2 + ...+ 180° - <аn= 180°n - ( <а1 + <a2 +...+ <an ) = 180°n- 180°(n-2) = 180°n - 180°n + 360°= 360°Bнешний угол прямого угла — также является прямым → наибольшее число прямых углов равно 360°:90° = 4 (иначе сумма внешних углов будет > 360°) →пример данного многоугольника - это прямоугольник или квадрат