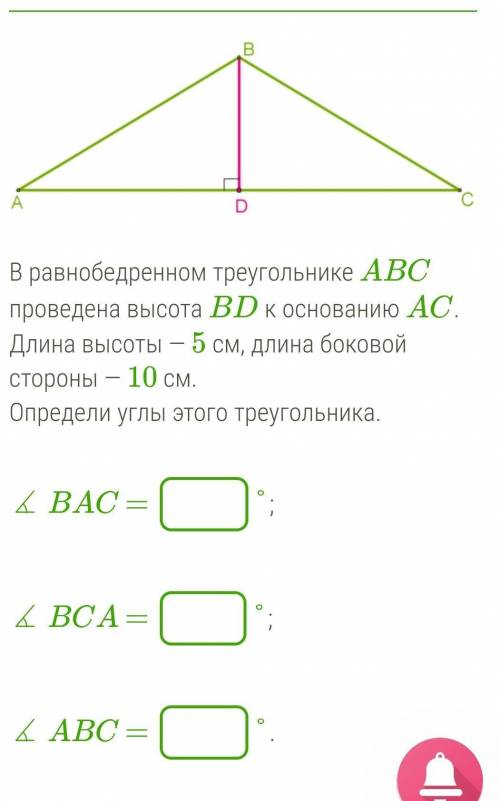
30 30 120
Объяснение:
Т.к BD - высота, то ∠BDA=90°, а значит треугольник BDC - прямой ⇒sin∠BCD =5/10=1/2 ⇒ ∠BCD=30°. Откуда ∠ABC=180-60=120°.
Можно по проще: катет BD равен половине гипотенузе BC ⇒ ∠BCD=30°
1200√3 см²
Объяснение:
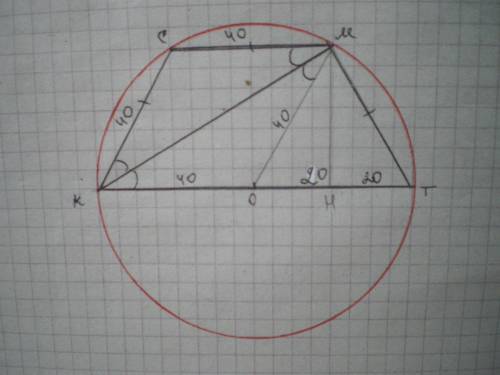
Дано: КСМТ - трапеція, КС=МТ, ∠КМТ=90°, КМ - бісектриса, ОМ=КО=ОТ=40 см. Знайти S(КСМТ).
∠КМТ - прямий, отже він спирається на діаметр описаного кола, тоді КТ=КО+ОТ=80 см.
∠СКМ=∠ТКМ за умовою, ∠СМК=∠ТКМ як внутрішні при СМ║КТ і січній КМ, отже ∠КСМ=∠СКМ, а ΔКСМ - рівнобедрений, КС=СМ.
Проведемо радіус ОМ=40 см, ΔКОМ=ΔКСМ за двома кутами і спільною стороною, отже КС=СМ=КО=ОМ=40 см.
МТ=КС=40 см.
ΔОМТ - рівнобедрений, проведемо МН - висоту і медіану.
ОН=ТН=40:2=20 см
За теоремою Піфагора МН=√(МТ²-ТН²)=√(1600-400)=√1200=20√3 см.
S(КСМТ)=(СМ+КТ):2*МН=(40+80):2*20√3=1200√3 см²
ответ: bac= 30, bca =30, abc =120
Объяснение: