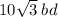
Объяснение:
1
a)М-середина
х=(5-3)/2=1 y=(-2+4)/2=1 z=(1+7)/2=4
M(1;1;4)
b)5=(x-3)/2⇒x-3=10⇒x=13
-2=(y+4)/2⇒y+4=-4⇒y=-8
1=(z+7)/2⇒z+7=2⇒z=-5
C(13;-8;-5)
2
a+b={1;-4;1}
|a+b|=√1+16+1=√18=3√2
|a|+|b|=√4+36+9+√1+4+4=√49+√9=7+3=10
3
AB=√(1-2)²+(-5-1)²+(0+8)²=√1+36+64=√101
BC=√(8-1)²+(1+5)²+(-4-0)²=√49+36+16=√101
AC=√(8-2)²+(1-1)²+(-4+8)²=√36+0+16=√52=2√13
AB=BC- треугольник равнобедренный
Средняя линия равна 1/2АС=1/2*2√13=√13
Пусть N(x;y;z)- произвольная точка плоскости.
Тогда векторы NM и n - ортогональны.
Условием ортогональности является равенство нулю их скалярного произведения.
Находим координаты векторов.
NM (2-x;3-y;5-z)
n(4;3;2)
Находим их скалярное произведение - это сумма произведений одноименных координат
4(2-х)+3(3-у)+2(5-z)
и приравниваем к нулю
4(2-х)+3(3-у)+2(5-z) =0
или
8-4х+9-3у+10-2z=0
4x+3y+2z-27=0
ответ. 4х+3у+2z-27=0
Подробнее - на -
рисунок1
треугольник АВС равнобедренный с основанием АС, поэтому углы при основании А и С равны по 20°. угол В равен 180°-2*20°=140°, высота ВD является и биссектрисой угла В, поэтому углы АВD и СВDравны по 140°/2=70°, при вершине D
углы прямые.
рисунок 2
угол. внешний угол АDВ равен сумме двух внешних. с ним не смежных ,т.е. 90°+15°=105°. Углы при вершине В равны, т.к. ВD - биссектриса, они равны по 15°, угол при вершине А равен 75°-15°=60°, ∠С=90°
Рисунок 3
Т.к. высота ВD и медиана, то углы А и С равны по 45°, как углы при основании равнобедренного треугольника АВС, а угол АВС равен 45°, т.к. ВD еще и биссектриса угла В