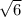
Объяснение:
Пусть BE - высота, проведенная к стороне AC, а точка D - равноудалена от концов AC, значит AD=DC. Рассмотрим тр-ки ADE и CDE. Они прямоугольные и у них один из катетов общий (DE), а гипотенузы равны AD=DC. Значит эти тр-ки равны: "если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны."
Из их равенства следует, что AE=EC, а значит тр-к ABC равнобедренный по признаку: "Если в треугольнике высота совпадает с медианой, то этот треугольник является равнобедренным"
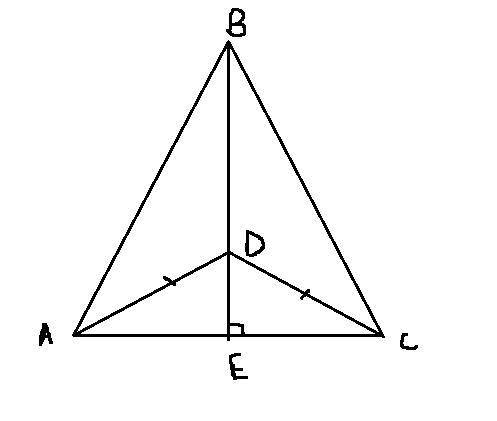
∠A = 90° => BD² = AB² + AD² (по теореме Пифагора)
26² = (5x)² + (12x)²
676 = 25x² + 144x²
676 = 169x²
x² = 676/169
x² = 4
x = 2
=> AB = 5x = 5 * 2 = 10 см; AD = 12x = 12 * 2 = 24 см
P ABCD = (10 + 24) * 2 = 68 см
ответ: 68 см