ответ: высота призмы=10см, Sбок.пов=900см²
Объяснение: чтобы найти боковую поверхность призмы необходимо взять найти площадь её оснований и вычесть. от общей площади.
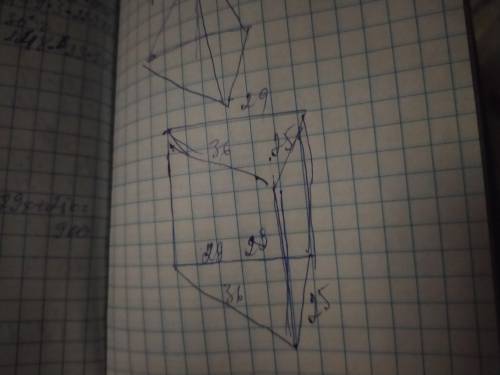
Найдём площадь основания по формуле Герона, используя полупериметр:
Р=25+29+36=90см;
р=90/2=45см
Sосн=√45((45-25)(45-29)(45-36))=
=√(45×20×16×9)=√129600=360см²
Итак: Sосн=360см²
Так как таких оснований 2, то площадь 2-х оснований= 360×2=720см²
S2-x=720см²
Sбок.пов=Sпол–S2осн=1620-720=900см²
Sбок.пов=900см².
Гранями призмы являются прямоугольники с разными сторонами, но в каждой грани есть общая сторона, которая является высотой призмы. Пусть высота поизмы=х, и зная площадь боковой поверхности составим уравнение:
25х+29х+36х=900
90х=900
х=900/90
х=10
Высота призмы=10см
Объяснение:
№6
1) NP = 10 - диаметр => радиус r=10/2 = 5
Рассмотрим ∆ KOP = р/б: OK=OP = r = 5 =>
=> <a = <OKP = 60° Сумма всех углов треугольника = 180° => третий угол равен 180-(60+60) = 60° => ∆KOP - равносторонний, правильный треугольник, и
KP= 5
2) Т.к все эти 3 угла равны между собой, а по рисунку мы видим, что они расположены ровно в половине окружности, т.е их сумма равна 180° =>
3x=180°
x=60° каждый угол. Возвращаясь к 1-вой задачи, мы видим равносторонний правильный треугольник со сторонами 12/2 = 6 => KP= 6.
3) не будем что-то там копать, просто рассмотрим ∆AOC - прямоугольный
по Т.П.: AC=√(16-4)=√12
рассмотрим ∆ ACN - прямоугольный
По Т.П.: AN= √(12+4) = √16 = 4
4) Рассмотрим ∆OAC - прямоугольный
< OAC=30° => по катет напротив угла в 30° равен половине гипотенузы: CO= AO/2 = 6/2 = 3
NC= 6-3 = 3
№9
P= *сумма длин всех сторон*
BN=BK;NK=AP;KC=CP
P= 6+4 + 4+6 + 12 = 32