Докажите, что середины сторон ромба являются вершинами прямоугольника
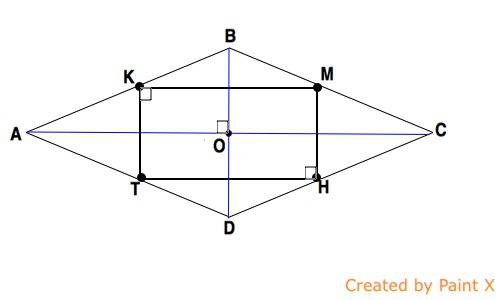
Пусть дан ромб АВСD, точки К, М, Н и Т - середины его сторон. Соединим их последовательно.
Диагонали ромба АС и ВD пересекаются под прямым углом и каждая делит ромб на два равных треугольника, a АК=КВ, ВМ=МС, СН=НD и DТ=ТА по условию. ⇒
КМ и ТН - средние линии равных треугольников АВС и СDТ и параллельны диагонали АС ромба. ⇒ КМ=ТН
Аналогично ТК и МН - средние линии треугольников АВD и СВD и параллельны диагонали ВD ромба. ⇒ КТ=МН.
Стороны четырехугольника ТКМН параллельны и равны - КМНТ - параллелограмм.
Диагонали ромба точкой их пересечения делятся пополам и, пересекаясь, делят четырехугольник ТКМН на 4 равных параллелограмма, углы которых при точке пересечения диагоналей ромба О прямые. ⇒
Углы К, М, Н и Т противоположны углам при О и по свойству углов параллелограмма равны им. Следовательно,
четырехугольник ТКМН - прямоугольник с вершинами в серединах сторон ромба, что и требовалось доказать.
В трехугольнике АСД угол С=90 градусов, угол Д=60, соответственно угол А=30 градусов. Так как АС биссектриса угла А трапеции, то угол САД=углу ВАС=30 градусов. Угол ВАД=60 градусов = углу Д. Трапеция равнобдренная АВ=СД. 2*СД=АД так как катет СД лежит против угла 30 градусов. Сумма углов трапеции равна 360 градусов. Угол В=углу С=(360-120)/2=120 градусов. В трехугольнике АВС угол С = 120-90=30 градусов. В этом же трехугольнике угол С=углу А - он равнобедренный. АВ=ВС. Соответственно, в трапеции АВСД АВ=ВС=СД. Периметр равен 3*АВ+АД. Так как 2*АВ=АД, то периметр равен 5*АВ=35 см. АВ=7 см.