Окружность с центром О.
ВС - диаметр.
А ∈ окружности с центром О.
∠АОС = 35°
Найти:∠ВАО - ?
Решение:
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
⇒ ∠ВАО + ∠ОВА = 35° (∠АОС = 35°, по условию)
Так как ∠ОВА = ∠ВАО, по свойству ⇒ ∠ОВА = ∠ВАО = 35°/2 = 17,5°
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Сумма смежных углов равна 180°.
∠АОС смежный с ∠ВОА ⇒ ∠ВОА = 180° - 35° = 145°
Сумма углов треугольника равна 180°.
⇒ ∠ВАО = ∠ОВА = (180° - 145°)/2 = 17,5°
ответ: 17,5°.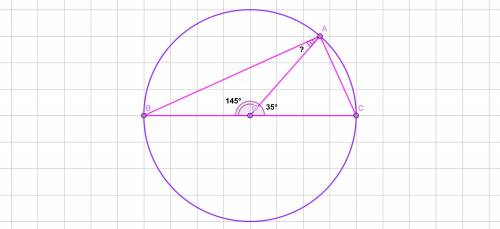
1) Шеңбердің радиусы тең болғандықтан, бұл ABO үшбұрышының екі жағы тең екенін білдіреді. ⇒ OABO изоцелдері (AO = OB).
Изоссельдер үшбұрышының негізіндегі бұрыштар тең, сондықтан: ∠OBA = ∠OAB = 30 °.
2) Шеңберге бағытталған тангенс CA ⊥ OA дегенді білдіретін тангенс нүктесіне бағытталған радиусқа перпендикуляр болады. ∠OAC = 90 °.
3) ∠BAC = ∠OAC - ∠OAB.
∠BAC = 90 ° - 30 ° = 60 °.
ЖАУАП: 60 °
1) ΔABO изотельдері, өйткені үшбұрыштың жақтарын құрайтын шеңбердің радиусы тең (AO = OB). Сондықтан ∠OBA = ∠OAB = 30 °.
Тангенс қасиеті бойынша CA ⊥ OA ⇒ ∠OAC = 90 °. Сонымен:
2) ∠BAC = 90 ° - 30 ° = 60 °
Диагонали ромба взаимно перпендикулярны и делятся в точке пересечения пополам.
В четвертинке ромба, образованного половинами диагоналей - прямоугольном тр-ке гипотенуза = стороне ромба = 25см, один катет (меньший) равен Х, а больший равен Х+5 (так как разность диагоналей равна 10, то разность их половин -5). По Пифагору Х²+(Х+5)²=25² или 2Х²+10Х-600=0 или Х²+5Х-300=0
Решаем квадратное ур-е и получаем: Х=(-5+√(25+1200))/2 = (5+35)/2 =20см
Отрицательное значение Х нас не устраивает. Значит диагонали ромба равны 40см и 50см.
Итак, площадь ромба равна 1/2(40*50) = 1000см²