В прямоугольном треугольнике АВС найти катет АС и высоту CD , если проекции катетов на гипотенузу АВ равны AD=25см, BD=4см.
Объяснение:
Если в прямоугольном треугольнике опущена высота на гипотенузу, то каждый из катетов есть среднее пропорциональное между всей гипотенузой и его проекцией на гипотенузу: АС=√(АВ*АD),
AC=√( (25+4)*25)=5√29 (см)
Если в прямоугольном треугольнике опущена высота на гипотенузу, то высота является средним пропорциональным между проекциями катетов на гипотенузу : CD=√AD*BD ,CD=√(25*4)=10 (см).

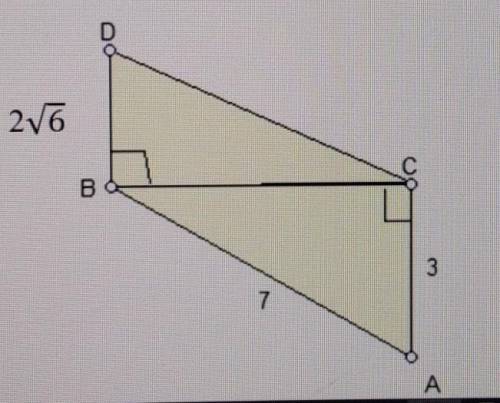
АВ^2 = АС^2 + ВС^2
49 = 9 + ВС^2
ВС^2 = 40
BC = √40
ВС = 2√10
Найдём DC по теореме Пифагора:
DC^2 = BD^2 + BC^2
DC^2 = 4 * 6 + 4 * 10 = 24 + 40 = 64
DC = 8
ответ: 8