Что и требовалось доказать!
Объяснение:Перпендикулярные прямые - прямые, которые пересекаются и при пересечении образуют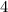 
прямых угла. (углы, градусная мера которых составляет 
).
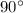Допустим, данные прямые перпендикулярны.
Тогда все три угла равны по .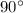
Сумма градусных мер трех неразвернутых углов, образованных при пересечение двух прямых, меньше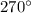 
, по условию.
Проверим: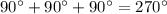 
Исходя из этого, мы доказали, что прямые не перендикулярны, так как сумма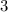 
неразвёрнутых углов составляет ровно 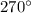, что не соответствует условию.
Что и требовалось доказать!
Объяснение:Перпендикулярные прямые - прямые, которые пересекаются и при пересечении образуют 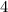прямых угла. (углы, градусная мера которых составляет ).
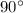Допустим, данные прямые перпендикулярны.
Тогда все три угла равны по .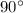
Сумма градусных мер трех неразвернутых углов, образованных при пересечение двух прямых, меньше 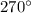, по условию.
Проверим: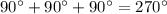
Исходя из этого, мы доказали, что прямые не перендикулярны, так как сумма 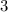неразвёрнутых углов составляет ровно 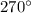, что не соответствует условию.
Объяснение:
Дано: FKPE - трапеция; FE = 24см; KP = 10см; FK=PE=9см.
Найти: ctg ∠F
Доп.построение: KA - высота, KA ⊥ FE
ctg - отношение прилежащего катета к противолежащему катету
ctg ∠F =
FA = (24-10)/2 = 7см
Найдём KA по т.Пифагора:
FK² = KA² + FA²
9² = KA² + 7²
KA² = 81 - 49 = 32
KA = √32
ctg ∠F = 7/√32