S полн = 72 см².
Объяснение:
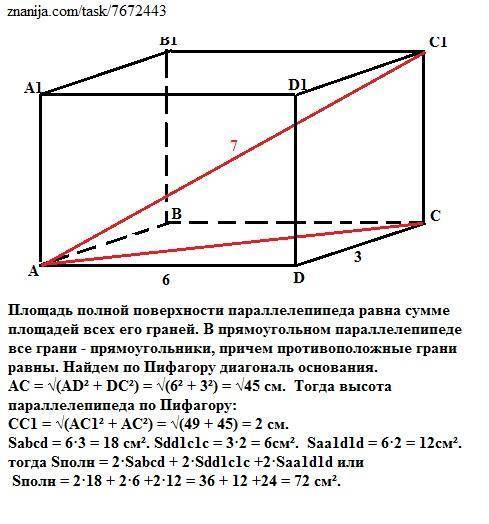
Площадь полной поверхности параллелепипеда равна сумме площадей всех его граней. В прямоугольном параллелепипеде все грани - прямоугольники, причем противоположные грани равны. Найдем по Пифагору диагональ основания.
АС = √(AD² + DC²) = √(6² + 3²) = √45 см. Тогда высота параллелепипеда по Пифагору:
СС1 = √(AС1² + АC²) = √(49 + 45) = 2 см.
Sabcd = 6·3 = 18 см². Sdd1c1c = 3·2 = 6см². Saa1d1d = 6·2 = 12см².
тогда Sполн = 2·Sabcd + 2·Sdd1с1с +2·Saa1d1d или
Sполн = 2·18 + 2·6 +2·12 = 36 + 12 +24 = 72 см².
В каждом из пунктов действуешь по теореме Пифагора, рассматривая треугольник АА1В, с прямым углом А1:
1) АА1^2+A1B^2=AB^2
16+A1B^2=25
A1B^2=9
A1B=3
2) AA1^2+BA1^2=AB^2
64+36=AB^2
AB^2=100
AB=10
3) AA1^2+A1B^2=AB^2
AA1^2+16=256
AA1^2=240
AA1=4 корня из 15