Объяснение:
обшая градус треугольника равна 180 градусов
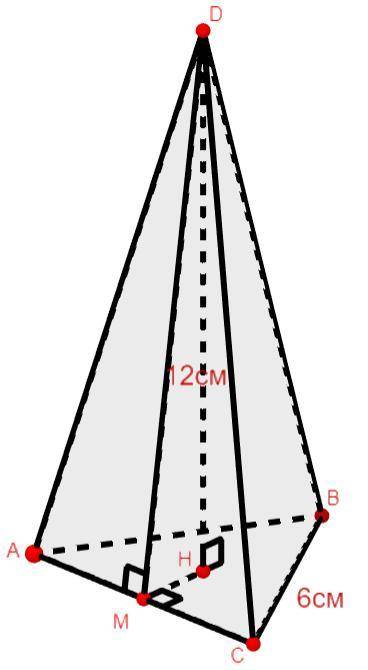
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)=
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
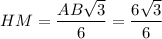=√3 см
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
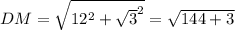=√147 см
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)=
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².
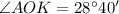
Объяснение:
Рассмотрим угол МОК он опирается на дугу окружности МК, угол МNK тоже опирается на эту дугу. Угол МОК центральный, а значит дуга МК равна этому углу и равна 78 градусам. Тогда угол МNK равен половине дуги, тк он не центральный, но вписанный и равен 39 градусам.
Теперь найдем смежный угол с углом МOK он равен: 180-78=102 градусам.
Теперь, зная что сумма углов в треугольнике равна 180 градусам то можем найти чему равен х, от 180 отнимаем 102 (это известный угол )и отнимаем 39(тоже известный угол)
И получаем: 180-102-39= 39 градусов( этот треугольник также получается равнобедренным поскольку углы при основани равны)
ответ:х = 39 градусов