Расстояние от точки до сторон квадрата равно 13 см. Найдите расстояние от точки до плоскости квадрата, если сторона квадрата равна 10 см. можете объяснить, с рисунком
Объяснение:
Расстояние от точки Т до плоскости отрезок ТО ⊥ ( АВС) . Значит ТО перпендикулярен любой прямой лежащей в плоскости.
Т.к. расстояние -это перпендикуляр, то опустим перпендикуляры из точки Т на стороны квадрата : ТН₁ , ТН₂ , ТН₃ , ТН₄. Тогда прямоугольные треугольники ( на рисунке желтые) равны по катету и гипотенузе ( апофема боковой грани).⇒точка О -центр вписанной окружности и еще т. пересечения диагоналей квадрата.
Н₁ Н₃= 10 , ОН₁=5 , из ΔТОН₁ , по т. Пифагора ТО=√(13³-5²)=√144=12 (см)
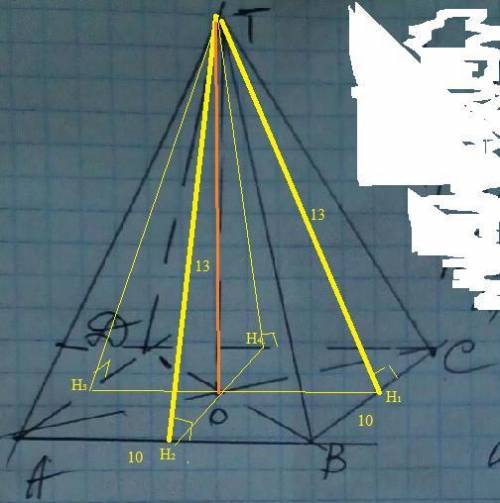
Рисунок на фото.
Дано: Δ ABC
∠ BAC = ?
∠ ABC = ?, в 2 раза больше —>∠ BAC
∠ BCA = ?, на 30° меньше —>∠ ABC
Найти: ∠ BAC = ?
∠ ABC = ?
∠ BCA = ?
Решение: Пусть, градусная мера ∠ BAC = x°, тогда ∠ ABC = (2x)°, а ∠ BCA = (2x - 30)°
x + 2x + (2x - 30) = 180
5x = 210
x = 42
Тогда ∠ BAC = 42°, ∠ ABC = 84°, а ∠ BCA = 54°,
Δ ABC – остроугольный потому, что все его углы меньше 90°.
ответ: ∠ BAC = 42°,∠ ABC = 84°, ∠ BCA = 54°;
Δ ABC – остроугольный.