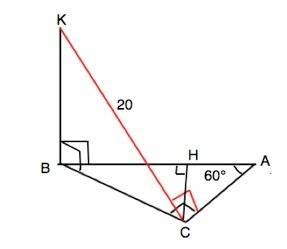
Сумма острых углов прямоугольного треугольника 90°⇒
∠АВС=90°-60°=30°
∆ ВСН прямоугольный, СН противолежит углу 30°.По свойству прямоугольного треугольника с углом 30° гипотенуза ВС = 2•СН=16 см
Расстояние от точки до прямой - длина отрезка, проведенного перпендикулярно к ней.
ВС⊥АС, ВС - проекция КС.
По т. о 3-х перпендикулярах КС⊥АС.⇒ КС - данное в условии расстояние от К до АС.
По условию ВК перпендикулярна плоскости АВС, следовательно, перпендикулярна любой прямой, проходящей через В. ⇒
∆ КВС прямоугольный,
По т.Пифагора КВ=√(KC²-BC²)=√(400-256)=12 см
Для обозначения геометрических фигур и их проекций, для отображения отношения между геометрическими фигурами, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем используются символьные обозначения.
- Большими латинскими буквами A, B, C, D, ..., L, M, N, ... - обозначают точки расположенные в пространстве;
- малыми латинскими буквами a, b, c, d, ..., l, m, n, ... - обозначают линии, расположенные в пространстве;
- малыми греческими буквами α, β, γ, δ, ..., ζ, η, θ - обозначают плоскости;
∈, ⊂ , ⊃ - Такими знаками обозначают принадлежность точек прямой и прямых плоскости
Теперь Задание:
1 точка M принадлежит плоскости альфа но не принадлежит плоскости бета
α, β, плоскости, М- точка
М∈α, М∉β
2 прямая l и точка N не лежащая на прямой l. принадлежат плоскости бета
N∉l; N∈α; l⊂α