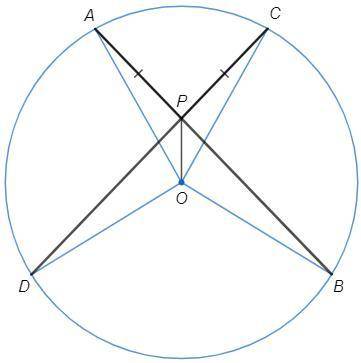
Хорды AB и CD пересекаются в точке P. AP=CP. Доказать, что AB=CD.
1) ∠DAB=∠BCD (=∪BD/2, вписанные) => △APD=△CPB (по стороне и прилежащим углам) => PD=PB
AP+PB=CP+PD => AB=CD
2) OA=OC=OB=OD (радиусы)
△OAP=△OCP (по трем сторонам) => ∠OAB=∠OCD
△AOB, △COD - равнобедренные
∠AOB =180-2∠OAB =180-2∠OCD =∠COD
△AOB=△COD (по двум сторонам и углу между ними) => AB=CD
Так как разность этих углов не равна нулю, значит эти углы не равны, следовательно они в сумме дают 180 градусов. Других углов, образованных при пересечении двух параллельных прямых секущей, не может быть. Эти углы - внутренние односторонние, найдем их градусные меры:
1) 180-42 = 138 град - удвоенный меньший угол
2) 138 : 2 = 69 град - меньший угол - один из внутренних односторонних углов
3) 69+42=111 град - больший угол - другой из внутренних односторонних углов
Остальные углы либо накрестлежащие с данными и они им равны, или соответственные с данными и они им тоже равны по свойству соответствующих углов.
Объяснение:
ДАНО: АВ ∩ СД = О,
АО = ОД; ОС = ОВ.
Решение. рассмотрим ΔАОД и ΔВОС: ∠О- общий АО:ОВ =ОД:ОС
ТАК КАК по условию стороны АО = ОД; ОС = ОВ. ,ΔАОД и ΔВОС подобны то ∠А=∠В=∠С=∠Д ( как углы внутренние накрест лежащие и при основании равнобедренных Δ ) ⇒ АД // ВС ⇒ АВ=СД , что и требовалось