Question

Решите один любой вариант на приложенной карточке. желательно с обьяснением как решали (такое отмечу как лучший ответ) тобиш вы получите 30(так работает этот сайт)

Answer 1

Вариант 1.

1.

Для начала найдём один из отрезков, полученным, делением гипотенузы высотою: отрезок BD.

Так как это высота, то отрезок образует 2 прямых угла: <BDA; <ADC.

Тоесть образуется 2 прямоугольных треугольника: ΔBDA; ΔADC.

По теореме Пифагора — BC равен:

$BC = \sqrt{AB^2-AD^2}\\BC = \sqrt{20^2-12^2} \Rightarrow BC = \sqrt{256}\\BC = 16sm.$

Чтобы найти всю гипотенузу BC — вычислим оставшийся отрезок DC.

Для этого нам нужна одна из формул вычисления высоты прямоугольного треугольника:

$\displaysytle\\H = \sqrt{c_1c_2}\\AD = \sqrt{BD*DC}\\AD^2 = BD*DC\\12^2 = 16*x\\x = 12^2/16\\x = 9sm.$

DC = 9; BD = 16 => BC = 9+16 = 25см.

По теореме Пифагора, AC равен:

$AC = \sqrt{BC^2-AB^2}\\AC = \sqrt{25^2-12^2}\\AC = \sqrt{481} \Longrightarrow AC = 21.9sm.$

Косинус угла равен отношению прилежащего катета к гипотенузе, то есть:

$\displaystyle\\\cos($

Вывод: AC = 21.9см; cos(<C) = 0.876.

2.

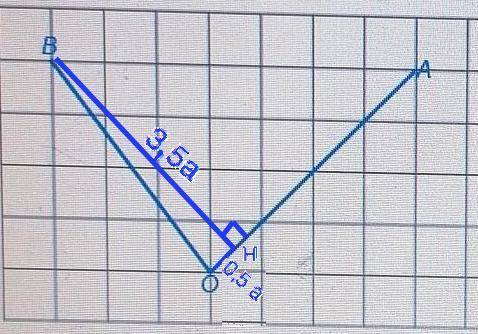
Для начала найдём оставшийся стороны паралеллограмма: BD & AD, которые друг другу равны.

Так как BD — перпендикулярен стороне AD — то он образует прямой угол с этой сторон, тоесть: ΔADB — прямоугольный.

Формула вычисления стороны BD, зная угол A, и гипотенузу AB: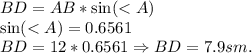 $BD = AB*\sin($

Осталось найти сторону AD (по теореме Пифагора), на которой проведена высота BD, чтобы потом найти площадь:

$AD = \sqrt{AC^2-BD^2}\\AD = \sqrt{12^2-7.9^2}\\AD = \sqrt{81.6} = 9sm.$

Теперь, формула вычисления площад параллелограмма такова: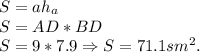 $S = ah_a\\S = AD*BD\\S = 9*7.9 \Rightarrow S = 71.1sm^2.$

Вывод: S = 71.1см².