Александрии, одно из семи чудес света
ответ: 6,6
Вариант решения.
Формула площади треугольника S=a•h/2 => h=2S:a.=>
Чем больше сторона треугольника, тем меньше высота, которая к ней проведена.
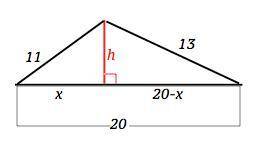
Пусть высота, проведенная к стороне 20, делит ее на отрезки х и 20-х, и образует два прямоугольных треугольника, гипотенузы которых - другие стороны исходного треугольника.
Выразим квадрат высоты из 1-го треугольника по т.Пифагора:
h²= 11²-х²
Аналогично – то же из второго треугольника:
h²=13²-(20-x)²
Приравняем эти значения
11²-х²=13²-(20-x)² Решив уравнение, получим
40х=352
х=8,8
Из меньшего треугольника по т.Пифагора
h=√(121-77,4)= 6,6 ( ед. длины)

Александрийский маяк был единственным из Семи чудес, имевшим практическое предназначение. Прежде всего, он давал возможность кораблям без проблем заплывать в порт Александрии, имевший важное стратегическое значение; кроме того, он служил дополнительным ориентиром морякам на фоне однообразного египетского побережья и, наконец, служил наблюдательным пунктом для наблюдения за водными просторами (военная угроза Александрии исходила в основном с моря, поскольку с суши город защищала пустыня).