Так. Приступим
синус угла А равен отношению противолежащего катета к гипотенузе. То есть sin A = 8/17
По теореме Пифагора найдем АС
АС = 15
синус угла B равен отношению противолежащего катета к гипотенузе. То есть sin B = 15/17
косинус угла A равен отношению прил.катета к гипотенузе,то есть 15/17
косинус угла B равен отношению прил катета к гипотенузе,то есть 8/17
тангенс угла А равен отношению противолежащего катета на прилежащий = 8/15
тангенс угла B равен отношению противолежащего катета на прилежащий = 15/8
котаангенс угла А равен отношению прилежащего катета на противолежащий = 15/8
котаангенс угла B равен отношению прилежащегоо катета на противолежащий = 8/15
Соединим центр окружности О с точками А и С. Полученный четырехугольник ВАОС- ромб, т.к. его диагонали ВО и АС пересекаются под прямым углом и делятся в точке пересечения пополам.Меньшая диагональ ромба равна радиусу окружности. Обозначим вторую диагональ 2х. По теореме об отрезках пересекающихся хорд получим
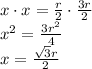
Эта диагональ делит наш ромб на два равных равнобедренных треугольника. Рассмотрим один из этих треугольников АОС. Используя теорему косинусов найдем косинус угла АОС.
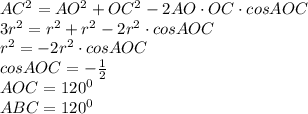
Угол АОС- центральный, а угол АDС - соответствующий ему вписанный, поэтому он равен половине центрального АОС, т.е. угол АDС=60 градусов.Углы ВАD и ВСD равны и равны 90 градусов, потому что они опираются на диаметр окружности. Таким образом углы четыврехугольника равны : угол В=120, угол D =60, угол А и угол С по 90. Так как центральные углы АОС, АОD и СОD равны и образуют вместе 360 градусов, то каждый из них равен 120 градусов. зная это определим градусную меру дуг. Дуга АВ = дуге ВС = 60 градусов. Дуга АD= дуге СD= 120 градусов.
Координаты середины равны полусумма соотвествующий координат концов
О((3-9)/2;(-7+8)/2)
О(-3;0,5)