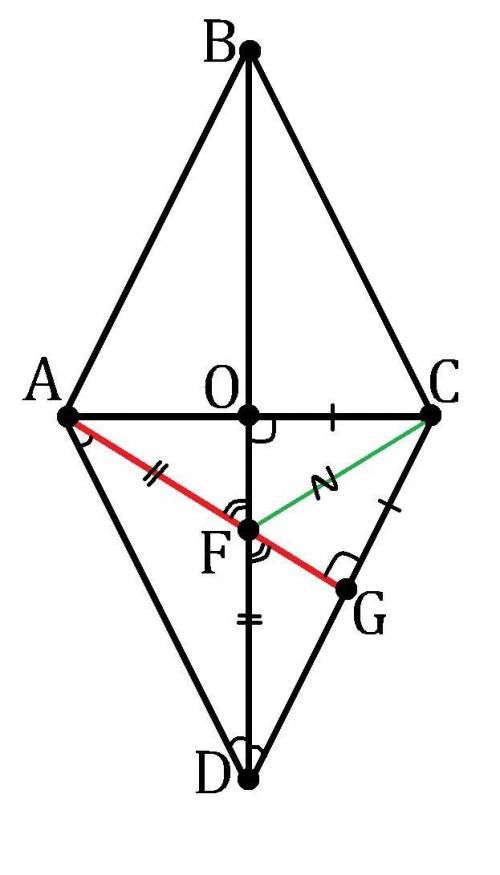
Дано: ABCD - ромб; AG⊥CD; AG=5см; BD=10см.
Найти: ∠(AG, BD).
Диагонали в ромбе служат биссектрисами углов, пересекаются под прямым углом и делятся точкой пересечения пополам.
Пусть AC∩BD=O, тогда OD = BD÷2 = 10÷2 = 5см.
Рассмотрим прямоугольные треугольники AGC и DOC:
AG = 5см = OD; ∠C - общий.
ΔAGC = ΔDOC по катету и острому углу, поэтому OC=GC.
Пусть AG∩OD=F.
Рассмотрим прямоугольные ΔFOC и ΔFGC:
FC - общая; OC=GC.
ΔFOC = ΔFGC по гипотенузе и катету, поэтому FO=FG.
Рассмотрим прямоугольные ΔAFO и ΔDFG:
∠AFO = ∠DFG как вертикальные; FO=FG.
ΔAFO = ΔDFG по катету и острому углу, поэтому AF=DF.
ΔAFD - равнобедренный (AF=DF), поэтому ∠DAF=∠ADF.
Пусть ∠СDF=x, тогда ∠ADF=x т.к. ∠CDF=∠ADF как углы при биссектрисе.
∠DAF=∠ADF=x.
Сумма углов в треугольнике равна 180°.
∠ADF+∠DAF+∠DFA=180°; ∠DFA=180°-∠ADF-∠DAF=180°-2x.
∠GDF+∠DFG+∠FGD=180°; ∠DFG=180°-∠FGD-∠GDF=90°-x.
Сумма смежных углов равна 180°.
∠DFG+∠DFA=180°=(90°-x)+(180°-2x)
270°-3x=180°; 3x=90°; x=30°.
∠DFG = 90°-x = 90°-30° = 60°.
Угол между пересекающимися прямыми не превышает 90°, 60°<90° ⇒ ∠(AG, BD) = ∠DFG = 60°.
ответ: 60°.
при построении перпендикуляра АЕ на диагональ ВД образуется прямоугольный треугольник АЕД Обозначим точку пересения диагоналей точкой О так как угол ДОА равен 30 градусов то по свойству прям треугольников угол ЕАО равен 60 градусам
перпендикуляр АЕ будет для ТРЕУГОЛЬНИКА АЕД катетом так как он расположен напротив угла 30 градусов то равен половине гипотенузе треугольника ЕАО отсюда следует что диагональ АС равна 4*АЕ так как АС равно ВД то ДИАГОНАЛЬ ВД равна 4*АЕ (если известно чему равно АЕ то можно подставить 4*АЕ)