а)Даны стороны треугольника АВ и АС и угол между ними.
На произвольной прямой отложим отрезок, равный длине стороны АС, отметим на нём точки А и С.
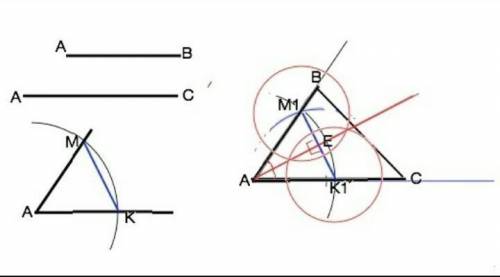
Из вершины А заданного угла проведем полуокружность произвольного радиуса и сделаем насечки М и К на его сторонах. АМ=АК= радиусу проведенной окружности.
Из т.А на отложенном отрезке тем же раствором циркуля проведем полуокружность. Точку пересечения с АС обозначим К1.
От К1 циркулем проведем полуокружность радиусом, равным длине отрезка КМ, соединяющим стороны заданного угла.
Эта полуокружность пересечется с первой. Через точку пересечения проведем от т. А луч и отложим на нем отрезок, равный данной стороне АВ, отметим точку В. . Соединим В и С.
Искомый треугольник построен.
б) Биссектриса проводится так же, как проводится срединный перпендикуляр к отрезку.
Из точек, взятых на сторонах угла на равном расстоянии от его вершины А ( отмеряем циркулем) проводим полуокружности равного радиуса так, чтобы они пересеклись. Через точки их пересечения и А проводим луч. Треугольник АМ1К! - равнобедренный по построению, АЕ - перпендикулярен М1К1 и делит его пополам.
Треугольники АЕМ1 и АЕК1 равны по гипотенузе и общему катету. Поэтому их углы при А равны. АЕ - биссектриса
2. Аксиома - математическое предложение, принимаемое без доказательства. В основе геометрии, (а по сути любой естественной науки) лежат несколько аксиом, которые приняли без доказательства, так как доказательство невозможно и они кажутся очевидными. Например, аксиома о том, что параллельные прямые не пересекаются в евклидовой геометрии лежит в основе той геометрии, которую мы изучаем в школе. 2 человека засомневались в верности этой аксиомы. Отказались от этой аксиомы и приняли аксиому, что параллельные прямые пересекаются. И построили свои геометрии, в которые евклидова входит как частный случай. Эти люди Лобачевский и Риман. Теперь есть кроме евклидовой еще геометрия Лобачевского и риманова геометрия. Вот такое дело аксиомы.
3. Аксиома параллельных прямых:
Через любую точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
Но вариантов формулировки этой аксиомы видимо-невидимо.