4,6
Объяснение:
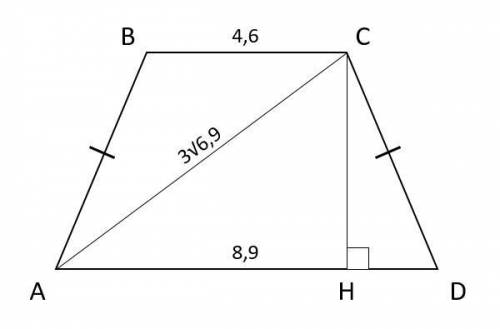
Дано: ABCD — трапеция, AB = CD, BC = 4,6, AD = 8,9, AC = 3√6,9
Найти: CD
1) Проведем высоту CH (CH⊥AD). Она разделила основание AD на два отрезка. Поскольку трапеция ABCD — равнобедренная (AB = CD), больший из них (AH) равен полусумме оснований:
AH = (AD+BC)/2 = (8,9+4,6)/2 = 13,5/2 = 6,75
Тогда DH = AD-AH = 8,9-6,75 = 2,15
2) ΔACH — прямоугольный (∠AHC = 90°), тогда по теореме Пифагора
AH²+CH² = AC², отсюда CH² = AC²-AH²
CH² = (3√6,9)²-6,75² = 62,1-45,5625 = 16,5375
3) ΔCHD — прямоугольный (∠CHD = 90°), тогда по теореме Пифагора
CH²+DH² = CD², отсюда CD = √(CH²+DH²)
CD = √(16,5375+2,15²) = √(16,5375+4,6225) = √21,16 = 4,6
Пусть ∠ В равен х°
Тогда ∠ А равен х+50°, а
∠ С (х+х+50):5
Составим уравнение, приравняв их сумму к 180°
2х+50+(2х+50):5=180
Умножим на 5, чтобы избавиться от дроби, обе части уравнения, и решим его.
10х++250+2х+50=900
12х=900-300
12х=600°
х=50°
Углы
∠В=50°
∠А=100°
∠С=150:5=30°
∠ВМА= 180-В-1/2А=180-50-50=80°
∠АМС=180-ВМА=180-80=100°