Ра А 1. Даны отрезок КМ; К(-2; 4), M (6; -2).
а) Вычислите длину отрезка КМ.
б) Постройте отрезок K,M, симметричный отрезку
км относительно оси ординат. Определите вид четы-
рехугольника КК¹ММ¹
в) Чему равны длины диагонали км, и средней ли
нии четырехугольника КК¹ММ¹?
г) Запишите уравнение окружности с центром в нача-
ле координат, проходящей через точку К.
2. Точки А (4; -1), В (2; -4), C (0; -1) являются верши-
нами параллелограмма ABCD.
а) Найдите координаты вершины D.
б) Докажите, что четырехугольник ABCD является
ромбом.
в) Напишите уравнения прямых, на которых лежат
диагонали четырехугольника ABCD.
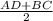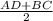* h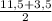
* 7,5 = 56,25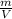
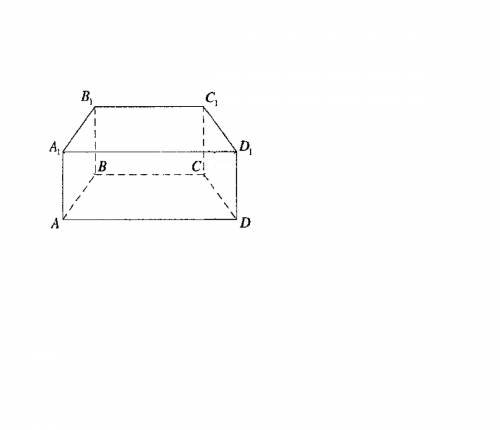
Основанием прямоугольного параллелепипеда ABCDA1B1C1D1 является квадрат,диагональ которого равна 12√2 дм. Диагональ боковой грани параллелепипеда равна 8√3 дм.
Вычислите градусную меру двугранного угла D1ABD
--------------------
Решение здесь очень короткое, в отличие от пояснения.
Сделаем рисунок. Двугранный угол, градусную меру которого нужно вычислить, составлен плоскостью ∆ D1АВ и плоскостью ∆ DАВ. Первая лежит в плоскости диагонального сечения параллелепипеда, другая - в плоскости его основания.
Величина двугранного угла равна его линейному углу, который образован двумя лучами, проведенными в каждой из плоскостей перпендикулярно одной точке на линии их пересечения.
D1А⊥АВ, DА⊥АВ⇒ искомый угол - угол D1АD.
Диагональ квадрата делит его на два равнобедренных треугольника. АD=АВ, и ВD =12√2
АD можно найти а) по т.Пифагора; б) через синус (косинус) 45º или просто вспомнить, что диагональ квадрата ( как и гипотенуза равнобедренного прямоугольного треугольника) равна а√2, где а - сторона квадрата или катет равнобедренного прямоугольного треугольника. ⇒
АD=12
cos ∠DAD1=DA:AD1
cos ∠DAD1=12:8√3=(√3):2 - это косинус 30º