Геометрия: іть зробити тести з геометрії. ДУЖЕ ВАЖЛИВО

іть зробити тести з геометрії. ДУЖЕ ВАЖЛИВО

👇

Открыть все ответы

Ответ:

Sashademin06

27.06.2022

1)Площадь трапеции находится по формуле: S= 0.5*( BC+AD) *BH, где BC и AD -основания, а BH- высота проведенная к AD.
2)Проведем из вершины C высоту CH1 к стороне AD, затем AH и H1D обозначим буквой x, они будут являться катетами прямоугольных треугольников ABH и CH1D.
3)Составим уравнение AD=BC+2x, т.к. HH1=BC
2x=AD-BC
x=21
4) Рассмотрим треугольник ABH:
AB=29( по условию);
AH=21( по доказанному);
AB^2= AH^2+BH^2
BH^2=841-441
BH=20
5)S= 0.5* ( 7+49) * 20
S=560
ответ: 560

4,4(58 оценок)

Ответ:

GeCUri

27.06.2022

Правильное условие:

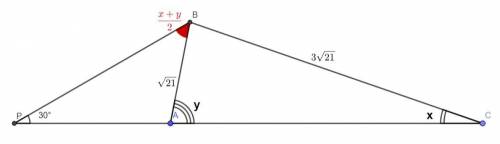
В треугольнике ABC AB=√21, BC=3√21. Биссектриса внешнего угла треугольника при вершине B пересекает прямую AC в точке P, угол APB равен 30°. Найдите BP.

Внешний угол треугольника равен сумме двух других не смежных с ним.

Пусть ∠CAB = y; ∠BCA = x.

Тогда внешний угол при вершине B равен x+y.

Биссектриса делит угол пополам, поэтому ∠ABP = 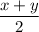$\dfrac{x+y}2$

По свойству внешнего угла из ΔAPB имеем:

∠CAB = ∠APB+∠ABP;

y = 30°+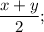 $\dfrac{x+y}2;$

2y = 60°+x+y;

y = 60°+x = ∠CAB.

В ΔABC, по теореме синусов, получим равенство:

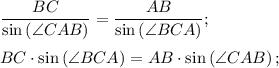
$\dfrac{BC}{\sin\left( \angle CAB\right) } =\dfrac{AB}{\sin\left( \angle BCA\right) };\\\\BC\cdot \sin\left( \angle BCA\right) =AB\cdot \sin\left( \angle CAB\right) ;$

3√(21)·sin(x) = √(21)·sin(60°+x);

3sin(x) = sin(60°)·cos(x)+cos(60°)·sin(x);

3sin(x) = 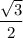$\dfrac{\sqrt3}2$ ·cos(x)+ $\dfrac12$ ·sin(x);

6sin(x)-sin(x) = 5sin(x) = √(3)·cos(x);

Если cos x = 0, то sin x = 0, но синус и косинус не могут одновременно равняться нулю, тогда поделим на cos x ≠ 0;

tg(x) = 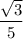$\dfrac{\sqrt3}5$ .

Найдём sin(x):

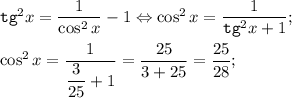
${\tt tg}^2x=\dfrac1{\cos ^2x}-1\Leftrightarrow \cos ^2x=\dfrac1{{\tt tg}^2x+1};\\\\\cos^2x=\dfrac1{\dfrac3{25}+1} =\dfrac{25}{3+25} =\dfrac{25}{28};$

По основному тригонометрическому тождеству:

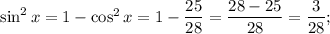
$\sin ^2x=1-\cos^2x=1-\dfrac{25}{28} =\dfrac{28-25}{28} =\dfrac3{28};$

sin(x) = +√(3/28) т.к. 0 < x < 180°, как угол треугольника.

По теореме синусов в ΔCPB:

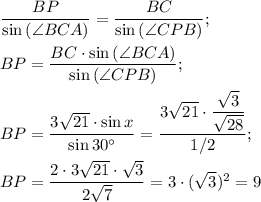
$\dfrac{BP}{\sin \left( \angle BCA\right) }=\dfrac{BC}{\sin \left( \angle CPB\right) };\\\\BP=\dfrac{BC\cdot \sin \left( \angle BCA\right) }{\sin \left( \angle CPB\right) };\\\\BP=\dfrac{3\sqrt{21}\cdot \sin x}{\sin 30^{\circ }} =\dfrac{3\sqrt{21}\cdot \dfrac{\sqrt3}{\sqrt{28}}}{1/2};\\\\BP=\dfrac{2\cdot 3\sqrt{21} \cdot \sqrt3}{2\sqrt7} =3\cdot (\sqrt3)^2=9$