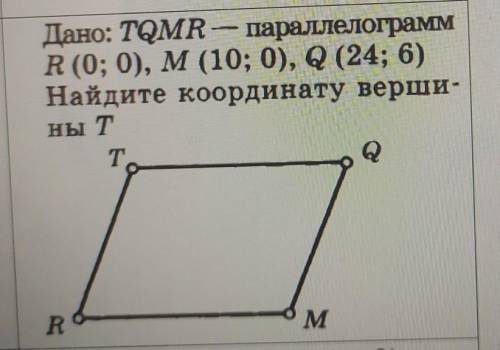
Построим сечение плоскостью через точки PMB
X - пересечение BP и AC
K - пересечение XM и DC
KMB - сечение
PT||BM, QT - искомый отрезок
В плоскости ABC:
проведем NY||BX
CY/YX =CN/NB =1
AY/YX =AN/NP =6/1
CY=YX=x, AY=6x, AC=5x => AC/CX =5/2
проведем NZ||AX
XZ/ZB =CN/NB =1
XZ/ZP =AN/NP =6/1
XZ=ZB=6x, ZP=x, PB=5x => XP/PB =7/5
В плоскости ADC:
AC/CX *XK/KM *MD/DA =1 (т Менелая) => 5/2 *XK/KM *1/2 =1 => XK/KM =4/5
В плоскости сечения KMB:
XT/TM =XP/PB =7/5 => TM/XM =5/12
XK/KM =4/5 => KM/XM =5/9
TM/KM =5/12 *9/5 =3/4 => KT/TM =1/4
QT/BM =KT/KM =1/4 => QT =1/4 a

Треугольники А0Д и В0С - подобные (уг.В0С = уг.А0Д как вертикальные; уг.СВ0 = уг.АД0 как внутренние накрест лежащие при параллельных прямых АД и ВС и секущей ВД).
Площадь тр-ка ВОС равна S1 = 0,5ВС·Н1
Площадь тр-ка АОД равна S2 = 0,5АД·Н2
При этом Н1:Н2 = к -коэфиициент подобия, а S1 : S2 = к²
S1 : S2 = 0,5ВС·Н1 : 0,5АД·Н2
к² = к· ВС: АД
к = 9/16
Итак, нашли коэффициент подобия.
Из подобия тех же тр-ков следует, что ОВ:ОД = 9/16, но ОД = АС - ОВ и
ОВ: (АС - ОВ) = 9/16
16·ОВ = 9·(АС - ОВ)
16·ОВ = 9·АС - 9·ОВ
25·ОВ = 9·АС
ОВ = 9·АС/25 = 9·18:25 = 6,48
ответ: ОВ = 6,48см
Объяснение: