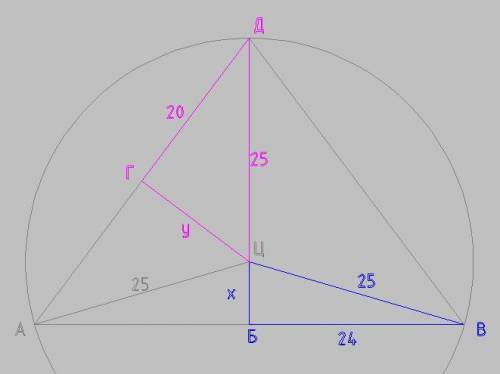
По формуле Герона вычислим площадь треугольника
полупериметр
p = (40 + 40 + 48)/2 = 40 + 24 = 64 см
Площадь
S² = p(p-a)(p-b)(p-c) = 64*(64-40)(64-40)(64-48) = 64*24²*16
S = √(64*24²*16) = 8*24*4 = 768 см
---
Радиус описанной окружности
R = abc/(4S) = 40*40*48 / (4 * 768) = 10 * 40 * 2 / 32 = 5 * 5 = 25 см
---
ΔАВЦ - равнобедренный, т.к. две его стороны - это радиусы описанной окружности ΔАВД
ЦБ - высота ΔАВЦ, одновременно и его биссектриса и сторону АВ делит пополам
БВ = АВ/2 = 48/2 = 24 см
По т. Пифагора для синего треугольника
БЦ² + БВ² = ВЦ²
х² + 24² = 25²
x² = 25² - 24² = (25 + 24)(25 - 24) = 49
x = 7 см
---
Аналогично по т. Пифагора для малинового треугольника
у² + 20² = 25²
y² = 25² - 20² = (25 + 20)(25 - 20) = 45*5 = 9*25
y = 3*5 = 15 см
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Верно. Аксиома планиметрии 9: через точку, не лежащую на данной прямой можно провести на плоскости не более одной прямой, параллельной данной.
2) Треугольник со сторонами 1,2,4 существует
Неверно. Длина каждой стороны треугольника не может быть больше или равна сумме двух других. 4>1+2 (неравенство треугольника)
3) Если в ромбе один из углов равен 90 гр, то такой ромб - квадрат
Верно. Сумма углов четырехугольника 360°. Ромб - параллелограмм, все стороны которого равны. Противоположные углы ромба равны. Если один угол равен 90°, противоположный равен 90°. Два других равны 90°. Квадрат - параллелограмм, все стороны которого равны (ромб) и все углы прямые (прямоугольник).