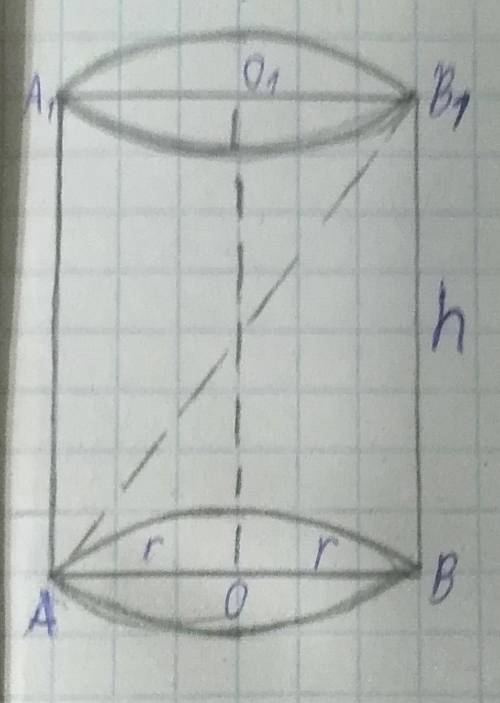
Дано:
цилиндр
AA₁B₁B - прямоугольник
r = AO = OB = 1 см - меньшая сторона прямоугольника
h = BB₁ = 3 см - большая сторона прямоугольника
-------------------------------------------------------------------------------------
Найти:
1. AB₁ - ?
2. Sполн - ?
1. Так как ΔABB₁ - прямоугольный (∠ABB₁ = 90°), тогда используется по теореме Пифагора:
AB₁² = AB² + BB₁² ⇒ AB₁ = √AB² + BB₁² - теорема Пифагора
AB = AO + OB = r + r = 2r = 2×1 см = 2 см
AB₁ = √(2 см)² + (3 см)² = √4 см² + 9 см² = √13 см² = √13 см
2. Давайте запишем формулу площади полной поверхности цилиндра, именно по такой формуле мы найдем площадь полной поверхности цилиндра:
Sполн = Sбок + 2Sосн = 2πrh = 2πr² = 2πr(h+r) = 2π×AO×(BB₁+AO) = 2π×1 см × (3 см + 1 см) = 2π см × 4 см = 8π см²
ответ: 1. AB₁ = √13 см
2.Sполн = 8π см²
P.S. Рисунок показан внизу↓
Постройте график функции f(x)= -x²-6x+5
Объяснение:
Это парабола ,ветви вниз . Координаты вершины
х₀=-в/2а, х₀=-(-6)/(-2)= -3 , у₀=-(-3)²-6*(-3) +5= 14 , ( -3; 14).
Доп.точки f(x)= -x²-6x+5:
х: -6 -5 -4 -2
у: 5 10 13 13.
1) f(x)=5 при х=0 , х=-6.
5= -x²-6x+5, -x²-6x=0 , x²+6x=0 , х(х+6)=0 , х=0 , х=-6.
f(x)=2 при x≈ 0,5 , x≈-6,5
2= -x²-6x+5, -x²-6x+3=0 , x²+6x-3=0 , D=48 ,x≈ 0,5 , x≈-6,5.
f(x)=-1 при x≈ 0,9 , x≈-6,9
-1= -x²-6x+5, -x²-6x+6=0 , x²+6x-6=0 , D=60 ,x≈ 0,9 , x≈-6,9 .
2) Нули функции f(x)=0 :
0= -x²-6x+5, x²+6x-5=0 , D=56 ,x=-3+√14 ≈0,74 , x=-3-√14 ≈-6,74 ,
Промежутки знакопостоянства функции :
f(x)>0 при -3-√14 <х< -3+√14 ;
f(x)<0 при х < -3-√14 и x>-3+ √14
3) Координаты вершины ( -3; 14). Ось симметрии х=-3
4) Наибольшее значение : f(x)=14.