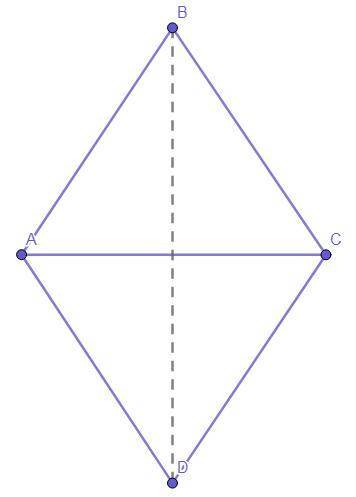
Четырёхугольник ABCD - ромб.
Отрезки АС и BD - диагонали.
АС = АВ.
Найти :Острый угол = ?
Решение :Ромб - это параллелограмм, у которого все стороны равны.
Поэтому -
АВ = ВС = CD = AD.
Рассмотрим ΔАВС.
АС = АВ = ВС.
Следовательно, ΔАВС - равносторонний (по определению равностороннего треугольника).
Каждый угол равностороннего треугольника равен по 60°.Отсюда -
∠ВАС = ∠В = ∠ВСА = 60°.
Диагональ ромба является биссектрисой его угла.То есть -
∠А = 60°*2 = 120°.
Противоположные углы параллелограмма равны.Следовательно -
∠В = ∠D = 60°
∠А = ∠С = 120°.
Отсюда острый угол ромба = 60°.
ответ :60°.
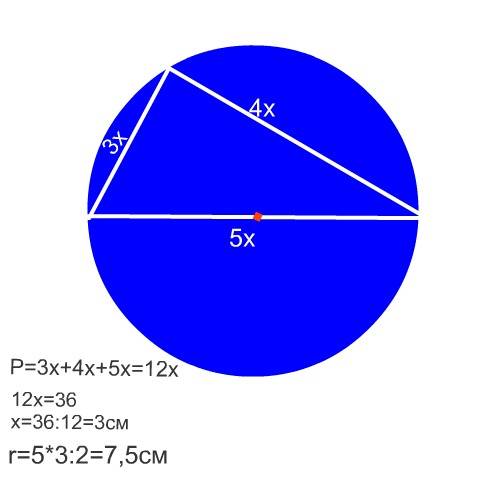
Гипотенуза этого прямоугольного треугольника является диаметром окружности.
Так как отношение катетов 3:4, то гипотенуза в этом отношении будет 5,
т.е все стороны треугольника относятся как 3:4:5, поскольку этот треугольник - египетский.
Примем коэффициент отношения сторон за х
тогда его периметр равен
3х+4х+5х=12х
Коэффициент равен 36:12=3
Диаметр круга
3*5=15 см
Радиус 15:2=7,5 см
-------------------------------
Боковую сторону можно найти через синус угла при вершине треугольника.
Он равен 180-2а
х=h: sin(180-2а)
35см; 56см
Объяснение:
Дано:
Окружности имеют внутреннее касание
О- центр большей окружности.
О1- центр меньшей окружности
ОО1=21 см расстояние между центрами окружностей.
r:R=5:8
R=?
r=?
Решение
Пусть радиус меньшей окружности будет 5х см, а болшей 8х см.
ОО1=R-r (расстояние между центрами окружностей при внешнем касании)
Уравнение.
8х-5х=21
3х=21
х=21/3
х=7
r=5*7=35 см радиус меньшей окружности
R=8*7=56 см радиус большей окружности