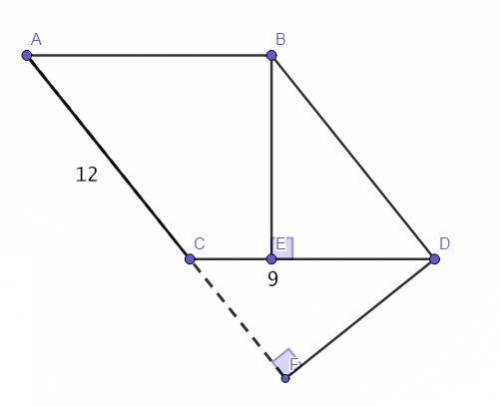
Чертёж смотрите во вложении.
Дано:
ABCD - параллелограмм.
CF - высота, опущенная из вершины ∠BCD на продолжение стороны AD.
ВЕ - высота, опущенная на сторону DC = 8.
DC (меньшая сторона) = 9.
AD (большая сторона) = 12.
Найти:
CF = ?
Площадь параллелограмма равна произведению стороны и высоты, опущенной на эту сторону.
В нашем случае -
S(ABCD) = DC*BE
S(ABCD) = 9*8
S(ABCD) = 72.
Но также формулу площади параллелограмма можно записать так -
S(ABCD) = СF*AD
Выразим через эту формулу значение CF -
CF = S(ABCD)/AD
Подставим в формулу известные нам значения -
CF = 72/12
CF = 6.
ответ: 6 (ед.измерения).
Радиус описанной окружности (R) = 21,25 см, радиус вписанной окружности (r) = 7 см
Объяснение:
1) Найдём площадь треугольника за формулой Герона:
S =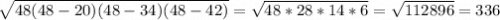 (см²)
(см²)
2) Находим радиус описанной окружности.
Выразим из формулы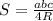 неизвестное R
неизвестное R
Получаем: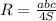
Подставляем числа в формулу и получаем:
3) Находим радиус вписанной окружности.
Выразим из формулы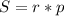 неизвестное r (p — полупериметр = 48 см)
неизвестное r (p — полупериметр = 48 см)
Получаем:
Подставляем числа в формулу и получаем:
Получаем: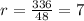 (см)
(см)
ответ: R = 21,25 см, r = 7 см