В равнобедренном треугольнике углы при основании равны. ∠ВАС=∠ВСА
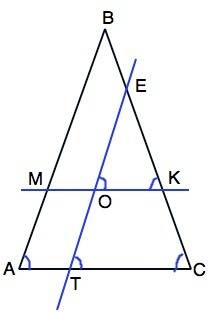
Обозначим данный треугольник АВС; О - точку пересечения прямых ЕТ||АВ и МК||АС.
АС секущая при ВА║ЕТ ⇒
∠ЕТС=∠ВАС как соответственные.
ЕТ секущая при МК║АС⇒
∠ЕОК=∠ЕТС как соответственные, следовательно, ∠ЕОК=∠ВАС.
ВС секущая при МК||АС⇒
∠ЕКО=∠ВСА, как соответственные. .
Следовательно, ∠ЕКО=∠ЕОК. что является признаком равнобедренного треугольника. ⇒
Треугольник ЕОК равнобедренный с углами при основании, которые равны углам при основании АС треугольника АВС.
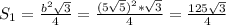
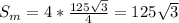
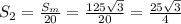
16 см и 30 см.
Объяснение:
Пусть в одной части х см, тогда
d1 = 8x см, а d2 = 15x см.
По теореме площадь ромба равна половине произведения его диагоналей, тогда
1/2 • 8х • 15х = 240
60х² = 240
х² = 240 : 60
х² = 4
х > 0, тогда х = 2.
d1 = 8•2= 16 (см)
d2 = 15•2= 30 (см)