Question

Кут між бічними сторонами рівнобедреного трикутника дорівнює 120°, бічна сторона - 4 см. Знайдіть радіус
описаного кола.

Answer 1

∆ АВС : АВ=ВС=4, <В =120°

углы при основании <А=<С= (180-120)/2=30°

Радиус описанного круга R=АВ/2 sin

С=4/2sin. 30=4/(2 * 1/2)=4

Answer 2

Радиус описанной окружности вокруг равнобедренного треугольника можно найти по формуле:

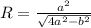$R = \frac{a^2}{\sqrt{4a^2 - b^2} }$, где а - боковые стороны треугольника, b - основа. Мы знаем боковые стороны, но не знаем основу. Так же нам дан угол между боковыми сторонами. Это даёт нам возможность использовать теорему косинусов:

$b^2 = a^2 + a^2 - 2aa *cos(\beta )$, где b - основа, a - боковое сторона, β - угол между боковыми сторонами.

Имеем:

$b^2 = 4^2 + 4^2 - 2 * 4 * 4 * cos(120^*)\\\\b^2 = 16 + 16 - 32*(-\frac{1}{2})\\\\b^2 =32 + 16\\\\b^2 = 48\\\\b = 4\sqrt{3}$

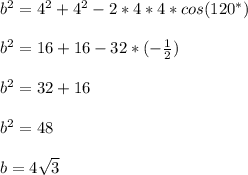
Теперь можно найти радиус:

$R = \frac{4^2}{\sqrt{4*4^2-(4\sqrt{3})^2 } } = \frac{16}{\sqrt{64-48} } = \frac{16}{\sqrt{16} } = \frac{16}{4} = 4$

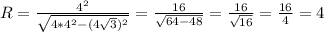
ответ: 4 см