Нужно построить прямоугольный треугольник, с циркуля и найти угол ∠AOC

Question

Геометрия: Нужно построить прямоугольный треугольник, с циркуля и найти угол ∠AOC

KseniaSob · Accepted Answer

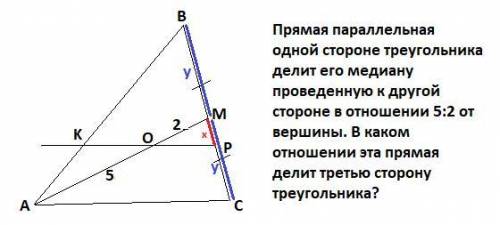
Прямая параллельная одной стороне треугольника делит его медиану проведенную к другой стороне в отношении 5:2 от вершины. В каком отношении эта прямая делит третью сторону треугольника?

Объяснение:

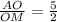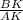Введем обозначения как показано на чертеже: КР║АС , ВМ=МС=у, МР=х . По условию $\frac{AO}{OM} =\frac{5}{2}$ . Необходимо найти $\frac{BK}{AK}$ .

Т.к. АС║КР , то по т. о пропорциональных отрезках 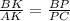$\frac{BK}{AK} =\frac{BP}{PC}$ или

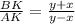$\frac{BK}{AK} =\frac{y+x}{y-x}$ (*) . По т. Менелая для ΔВАМ :

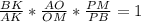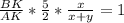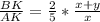$\frac{BK}{AK} *\frac{AO}{OM}* \frac{PM}{PB} =1$ или $\frac{BK}{AK} *\frac{5}{2}* \frac{x}{x+y} =1$ или $\frac{BK}{AK} =\frac{2}{5}* \frac{x+y}{x}$ (**).

Приравняем правые части (*) и (**) : 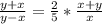$\frac{y+x}{y-x} =\frac{2}{5}* \frac{x+y}{x}$ или 2(у-х)=5х или

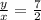$\frac{y}{x} =\frac{7}{2}$ .

Вернемся к (**) 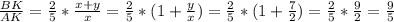$\frac{BK}{AK} =\frac{2}{5}*\frac{x+y}{x}=\frac{2}{5}*(1+\frac{y}{x} )=\frac{2}{5}*(1+\frac{7}{2} )=\frac{2}{5}*\frac{9}{2} =\frac{9}{5}$ .

Прямая параллельная одной стороне треугольника делит его медиану проведенную к другой стороне в отно

MOGZ ответил